Главная страница Предыдущая страница
2.3 Система линейных уравнений
Пусть дана система линейных уравнений
|
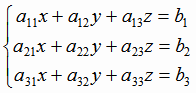(1.19) |
Определитель третьего порядка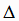 
, составленный из коэффициентов при неизвестных, называется определителем
системы:
 |
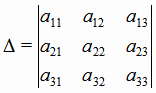(1.20) |
Различают следующие случаи (теорема Крамера):
1. Если определитель 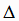системы (1.19) отличен от нуля, то система имеет, и притом единственное,
решение, которое может быть найдено по формулам Крамера:
 ,  ,  , |
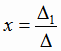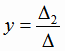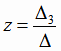(1.21) |
где определитель третьего порядка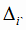 
(i = 1, 2, 3) получается из 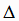путем замены i-того
столбца свободными членами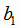 
, 
, 
:
; 
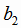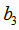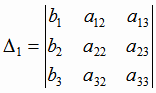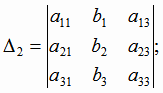
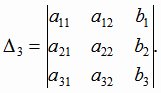
2. Если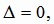 
но хотя бы один из
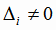(i = 1, 2, 3), то система (1.19)
несовместна (не имеет решений).
3. Есл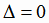и 
и
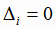(i = 1, 2, 3), то система (1.19) либо несовместна,
либо имеет бесконечное множество решений.