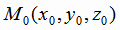 и вектор n = (A,B,C);
и вектор n = (A,B,C); 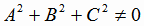 .
(Напомним, что координатами точки
.
(Напомним, что координатами точки 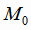 называются координаты её радиус-вектора
называются координаты её радиус-вектора  , где O - начало
координат). Тогда в пространстве однозначно определена плоскость π , проходящая через точку
, где O - начало
координат). Тогда в пространстве однозначно определена плоскость π , проходящая через точку 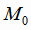 перпендиулярно вектору
n (рис. 1.5).
перпендиулярно вектору
n (рис. 1.5).Главная страница Предыдущая страница
2.2 Прямая и плоскость в пространстве
Пусть в пространстве фиксирована точка 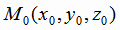 и вектор n = (A,B,C);
и вектор n = (A,B,C); 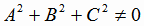 .
(Напомним, что координатами точки
.
(Напомним, что координатами точки 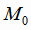 называются координаты её радиус-вектора
называются координаты её радиус-вектора  , где O - начало
координат). Тогда в пространстве однозначно определена плоскость π , проходящая через точку
, где O - начало
координат). Тогда в пространстве однозначно определена плоскость π , проходящая через точку 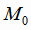 перпендиулярно вектору
n (рис. 1.5).
перпендиулярно вектору
n (рис. 1.5).
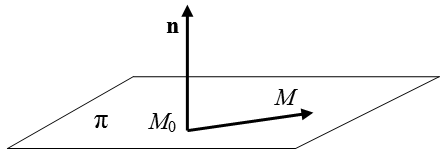
Рис. 1.5.
Уравнение этой плоскости имеет вид:
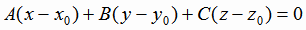 , , |
(1.7) |
где (x,y,z) - координаты произвольной точки М на плоскости π . Верно и обратное: если плоскость π задана уравнением
| Ax+ By+ Cz +D = 0, | (1.8) |
то вектор n = (A,B,C) ортогонален плоскости π . Вектор n называется нормальным вектором плоскости (1.8).
Пусть две плоскости 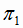 и
и 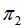 заданы уравнениями:
заданы уравнениями:
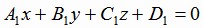 и
и 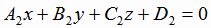 .
.
Угол φ между этими плоскостями очевидно равен углу между их нормальными векторами n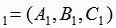 и n
и n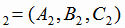 и определяется по формуле (1.3):
и определяется по формуле (1.3):
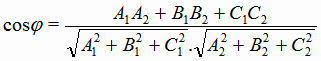 |
(1.9) |
Плоскость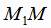 в пространстве можно однозначно задать с помощью трех её различных точек
в пространстве можно однозначно задать с помощью трех её различных точек 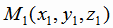 ,
,
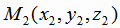 и
и 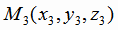 , не лежащих на одной прямой. Уравнение указанной плоскости можно записать, используя формулу
(1.7), где за нормальный вектор n можно взять векторное произведение векторов
, не лежащих на одной прямой. Уравнение указанной плоскости можно записать, используя формулу
(1.7), где за нормальный вектор n можно взять векторное произведение векторов 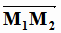 и
и 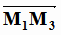 или
любой вектор, коллинеарный этому векторному произведению; а за точку
или
любой вектор, коллинеарный этому векторному произведению; а за точку 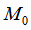 - любую из точек
- любую из точек 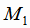 ,
, 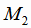 ,
,
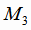 .
.
Другой прием получения уравнения плоскости 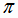 состоит в том, что записывается условие компланарности
векторов
состоит в том, что записывается условие компланарности
векторов 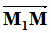 ,
, 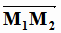 и
и 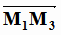 , где М - произвольная точка плоскости
с координатами (x, y, z) (рис.1.6):
, где М - произвольная точка плоскости
с координатами (x, y, z) (рис.1.6):
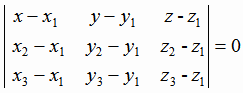 . .  |
(1.10) |
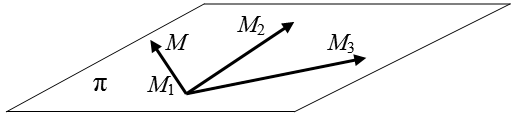
Рис. 1.6
Расстояние h от точки 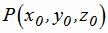 до плоскости, заданной уравнением (1.8), вычисляется
по формуле:
до плоскости, заданной уравнением (1.8), вычисляется
по формуле:
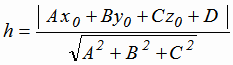 |
(1.11) |
Пусть в пространстве фиксирована точка 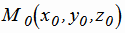 и вектор
и вектор 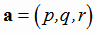 ;
; 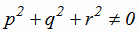 .
Тогда в пространстве однозначно определена прямая Г, проходящая через точку
.
Тогда в пространстве однозначно определена прямая Г, проходящая через точку 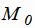 параллельно вектору a (рис.
1.7). Вектор a называется направляющим вектором этой прямой. Уравнения данной прямой имеют вид:
параллельно вектору a (рис.
1.7). Вектор a называется направляющим вектором этой прямой. Уравнения данной прямой имеют вид:
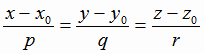 , , |
(1.12) |
где точка 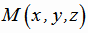 лежит на прямой Г.
лежит на прямой Г.
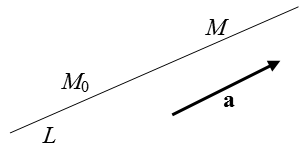
Рис. 1.7
Уравнения (1.12) принято называть каноническими уравнениями прямой. Заметим, что в уравнениях (1.12) одно или два из чисел p, q и r могут оказаться равными нулю. Тогда пропорцию (1.12) понимают так: обращение в нуль одного из знаменателей пропорции означает обращение в нуль и соответствующего числителя.
Из канонических уравнений прямой легко получаются параметрические уравнения:
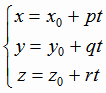 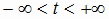 , , |
(1.13) |
где
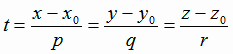
Вычисление угла между прямыми в пространстве сводится к вычислению угла между их направляющими векторами 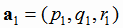 и
и 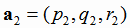 :
:
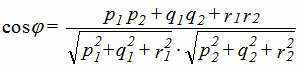 |
(1.14) |
Уравнения прямой, проходящей через две различные точки 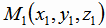 и
и 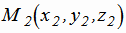 имеют вид:
имеют вид:
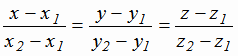 |
(1.15) |
Угол α между плоскостью 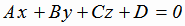 и прямой
и прямой 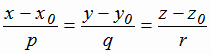 находится с помощью
угла
находится с помощью
угла 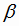 между нормалью к плоскости n и направляющим вектором прямой a:
между нормалью к плоскости n и направляющим вектором прямой a:
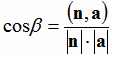
Если 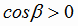 , т.е. угол
, т.е. угол 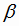 острый (рис. 1.8), то
острый (рис. 1.8), то 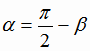 и
и 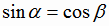 . Если
. Если 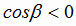 , т.е. угол
, т.е. угол 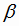 тупой (рис. 1.9), то
тупой (рис. 1.9), то 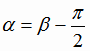 и
и 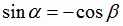 . Объединяя оба случая, получаем:
. Объединяя оба случая, получаем:
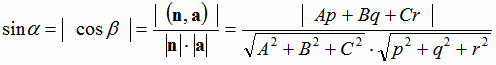 |
(1.16) |
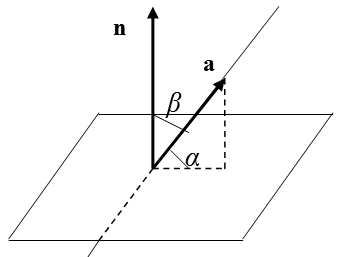
Рис. 1.8
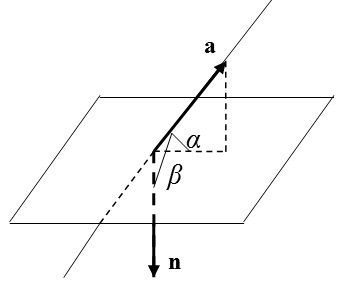
Рис. 1.9
Расстояние L от точки 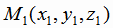 до прямой, заданной уравнением (1.12), вычисляется по формуле:
до прямой, заданной уравнением (1.12), вычисляется по формуле:
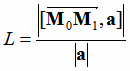 |
(1.17) |
Две прямые
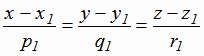 и
и 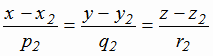
лежат в одной плоскости тогда и только тогда, когда равно нулю смешанное произведение:
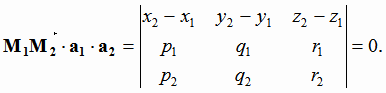
В противном случае прямые скрещиваются. Расстояние между скрещивающимися прямыми вычисляется по формуле:
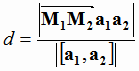 |
(1.18) |