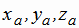 ), т.е.
), т.е. 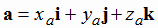 , где числа xa ,
ya , za --проекции вектора a на соответствующие оси координат. Пусть вектор b
имеет в том же базисе координаты( xb , yb , zb )
, где числа xa ,
ya , za --проекции вектора a на соответствующие оси координат. Пусть вектор b
имеет в том же базисе координаты( xb , yb , zb )Главная страница Предыдущая страница
2 Теоретическое введение
2.1 Векторная алгебра
Пусть в трехмерном пространстве задана декартова правая прямоугольная система координат OXYZ, пусть i, j, k
- соответствующие единичные орты. Тогда любой вектор, который мы будем обозначать символом a (рис. 1.1) однозначно задается в базисе
i, j, k координатами (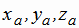 ), т.е.
), т.е. 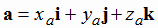 , где числа xa ,
ya , za --проекции вектора a на соответствующие оси координат. Пусть вектор b
имеет в том же базисе координаты( xb , yb , zb )
, где числа xa ,
ya , za --проекции вектора a на соответствующие оси координат. Пусть вектор b
имеет в том же базисе координаты( xb , yb , zb )
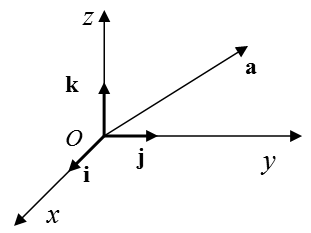
Рис. 1.1
Cкалярное произведение (a,b) двух векторов a и b равно произведению длин этих векторов
на косинус угла 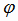 между ними (рис. 1.2) :
между ними (рис. 1.2) :
(a,b) = | a | · | b | · cos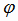 ,
, 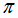
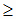
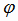

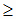 0.
0.
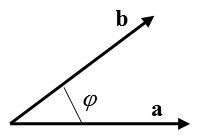
Рис. 1.2.
Скалярное произведение векторов вычисляется по формуле
| ( a, b ) = xa xb + ya yb + za zb , | (1.1) |
из которой, в частности, следует формула вычисления длины вектора
| a | = 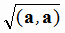 = =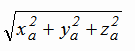 |
(1.2) |
Из формул (1.1) и (1.2) вытекает формула вычисления косинуса угла между векторами:
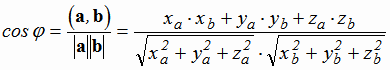 |
(1.3) |
Векторным произведением вектора a на вектор b называется такой вектор d = [a,b], длина и направление которого определяются условиями
1) |d| = |a|· |b| sin φ , где φ - угол между a и b,
2) d ^ a, d ^ b,
3) векторы a, b, d образуют правую тройку векторов, т.е. вектор d направлен так, что кратчайший поворот от a к b виден с его конца совершающимся против часовой стрелки.
Замечание: Если векторы a, b, c приведены к общему началу и кратчайший поворот от a к b виден с конца вектора с совершающимся по часовой стрелке, то векторы a, b, c образуют левую тройку векторов.
Если известны координаты векторов a и b, то координаты их векторного произведения [a,b] можно найти по формуле:
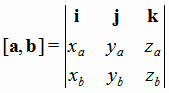 = =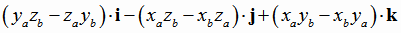 |
(1.4) |
Геометрический смысл векторного произведения состоит в том, что модуль вектора d = [a,b] численно равен площади параллелограмма, построенного на векторах a и b, вектор d направлен перпендикулярно плоскости, в которой лежат векторы a и b (рис. 1.3):
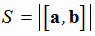 |
(1.5) |
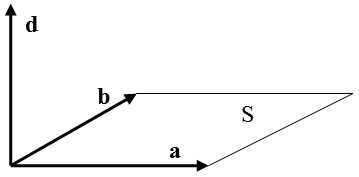
Рис. 1.3
Пусть даны три произвольных вектора a, b, c. Если вектор a векторно умножить на вектор b, а затем получившийся при этом вектор [a,b] скалярно умножить на вектор c, то в результате получится число ([a,b],c), называемое смешанным произведением векторов a, b, c и обозначаемое abc.
Смешанное произведение равно объёму V параллелепипеда, построенного на приведенных к общему началу векторах a, b, c, взятому со знаком "плюс", если тройка векторов a, b, c - правая и со знаком "минус", если эта тройка левая (рис. 1.4). Если же векторы a,b,c компланарны, то abc равно нулю.
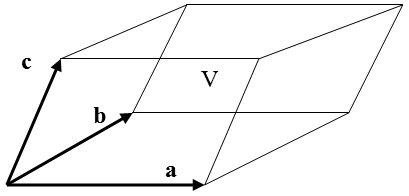
Рис. 1.4
Пусть векторы a, b, c определены своими декартовыми прямоугольными координатами
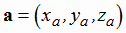 ;
; 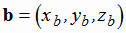 ;
; 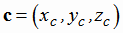 .
.
Тогда смешанное произведение abc равно определителю, строки которого соответственно равны координатам перемножаемых векторов:
 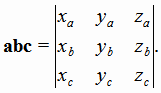 |
(1.6) |