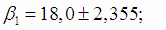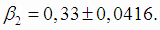Главная страница Предыдущая страница
3 Пример выполнения типового расчёта
3.1 Задача 1
Результаты эксперимента представлены в первых двух столбцах таблицы 4.1. По отдельной серии из n1=19
экспериментов найдена оценка дисперсии S2=0,96. Найдем оценки параметров линейной регрессии Y на х.
Таблица 4.1
Исходные данные и результаты расчёта (к задаче 1)
| x |
Y |
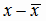 |
Х |
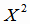
|
 |
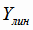 |
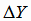 |
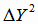 |
| 5 |
19,1 |
-45 |
-9 |
81 |
-171,9 |
19,65 |
-0,55 |
0,3025 |
| 20 |
25,4 |
-30 |
-6 |
36 |
-152,4 |
24,6 |
0,8 |
0,64 |
| 40 |
33,0 |
-10 |
-2 |
4 |
-66,0 |
31,2 |
1,8 |
3,24 |
| 50 |
34,1 |
0 |
0 |
0 |
0 |
34,5 |
-0,4 |
0,16 |
| 55 |
35,0 |
5 |
1 |
1 |
35,0 |
36,15 |
-1,15 |
1,3225 |
| 65 |
38,0 |
15 |
3 |
9 |
114,0 |
39,45 |
-1,45 |
2,1025 |
| 75 |
42,4 |
25 |
5 |
25 |
212,0 |
42,75 |
-0,35 |
0,1225 |
| 90 |
49,0 |
40 |
8 |
64 |
392,0 |
47,7 |
1,3 |
1,69 |
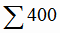 |
276 |
0 |
0 |
220 |
362,7 |
|
0 |
9,58 |
Сначала найдем решение задачи регрессии в кодированных значениях переменной х (4.14). Введем новую переменную по формуле
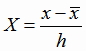 ,
,
где
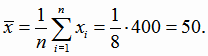
Значения величины 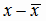 являются целыми числами с общим множителем h =
5. Поэтому переменная
являются целыми числами с общим множителем h =
5. Поэтому переменная 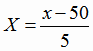 принимает целые значения, не имеющие общего множителя.
принимает целые значения, не имеющие общего множителя.
По формулам (4.15) находим оценки коэффициентов линейной регрессии
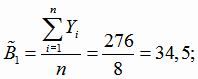
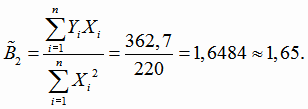
Получили линейную модель регрессии
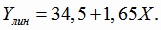 |
(4.30) |
Вычисляем значения линейной функции регрессии  по формуле (4.30) при всех значениях аргумента Х,
а затем рассчитываем
по формуле (4.30) при всех значениях аргумента Х,
а затем рассчитываем 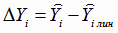 отклонения экспериментальных значений
отклонения экспериментальных значений 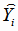 от значений
от значений 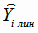 , полученных по функции регрессии, и, для контроля, суммируем значения
, полученных по функции регрессии, и, для контроля, суммируем значения
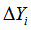 .
Условие (4.16) выполняется.
.
Условие (4.16) выполняется.
Далее суммируем значения 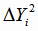 для нахождения дисперсии адекватности (4.17). Все расчёты приведены в таблице 4.1.
для нахождения дисперсии адекватности (4.17). Все расчёты приведены в таблице 4.1.
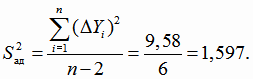
Проверяем адекватность линейной модели регрессии, используя критерий Фишера (4.11).
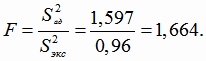
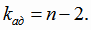
Квантиль распределения Фишера 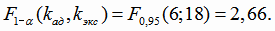 Так как
Так как
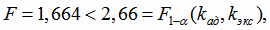
то гипотеза об адекватности линейной модели регрессии принимается.
Найдем доверительные интервалы для коэффициентов регрессии. Границы доверительных интервалов для коэффициентов В1 и В2
найдем по формулам (4.18). Так как линейная модель регрессии адекватна, в качестве оценки дисперсии возьмем дисперсию адекватности.
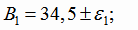
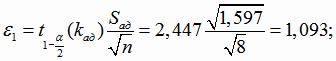
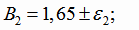
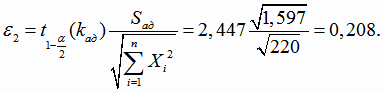
Уравнение линейной регрессии Y от исходного переменного х найдем, сделав преобразование:
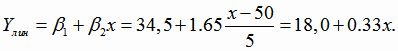 |
(4.31) |
Границы доверительных интервалов для коэффициентов β1 и β2 (4.18):

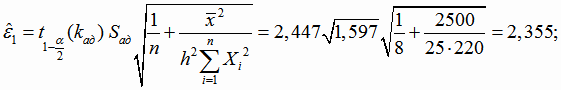
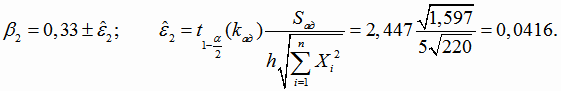
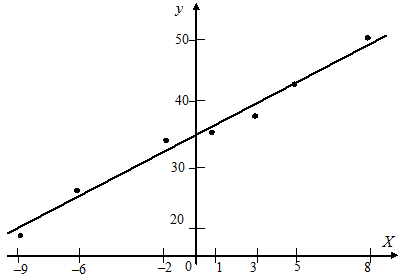
Рис. 4.1. График линейной модели регрессии
На рис. 4.1 построен график линейной модели регрессии. Точками помечены результаты эксперимента. На рисунке 4.2 приведен график отклонений
экспериментальных данных от функции регрессии. Отклонения носят хаотический характер, что подтверждает адекватность полученной модели.

Рис. 4.2. График отклонений экспериментальных данных от линейной функции регрессии.
Выводы по работе. По приведенным исходным данным методом наименьших квадратов построена адекватная линейная модель
регрессии с уровнем значимости α = 0,05,
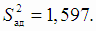
Уравнение регрессии в кодированных значениях переменной 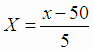 :
:

где 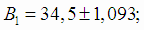

Уравнение регрессии в исходной переменной х:
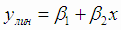 ,
,
где 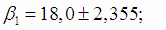
Следующая страница
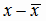

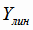
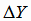
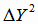
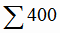
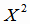
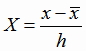 ,
, 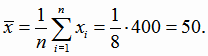
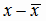 являются целыми числами с общим множителем h =
5. Поэтому переменная
являются целыми числами с общим множителем h =
5. Поэтому переменная 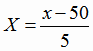 принимает целые значения, не имеющие общего множителя.
принимает целые значения, не имеющие общего множителя.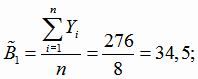
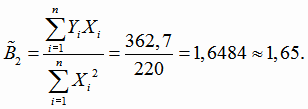
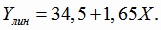
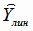 по формуле (4.30) при всех значениях аргумента Х,
а затем рассчитываем
по формуле (4.30) при всех значениях аргумента Х,
а затем рассчитываем 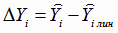 отклонения экспериментальных значений
отклонения экспериментальных значений 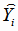 от значений
от значений 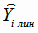 , полученных по функции регрессии, и, для контроля, суммируем значения
, полученных по функции регрессии, и, для контроля, суммируем значения
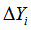 .
Условие (4.16) выполняется.
.
Условие (4.16) выполняется.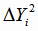 для нахождения дисперсии адекватности (4.17). Все расчёты приведены в таблице 4.1.
для нахождения дисперсии адекватности (4.17). Все расчёты приведены в таблице 4.1.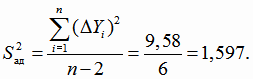
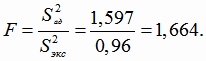
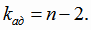
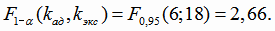 Так как
Так как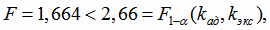
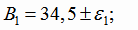
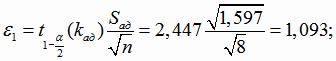
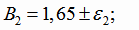
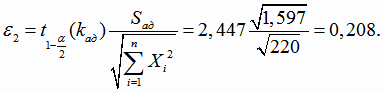
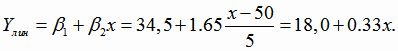

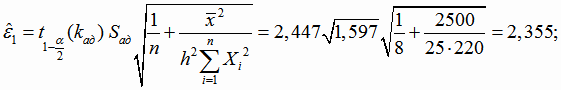
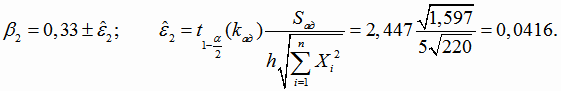
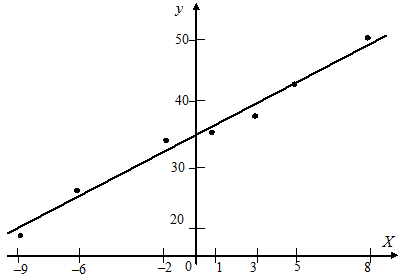

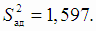
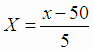 :
:
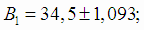

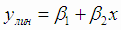 ,
,