Главная страница Предыдущая страница
3.2 Задача 2
Результаты эксперимента представлены в первых двух столбцах таблицы 4.2. По отдельной серии из
n2=20
экспериментов найдена оценка дисперсии S2=0,176. Найдем оценки параметров линейной регрессии Y на х.
Таблица 4.2
Исходные данные и результаты расчёта линейной модели регрессии (к задаче 2)
| х |
Y |
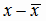 |
Х |
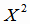
|
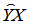 |
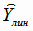 |
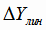 |
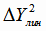 |
| 0 |
12,28 |
-0,5 |
-5 |
25 |
-61,4 |
14,923 |
-2,643 |
6,9854 |
| 0,2 |
18,66 |
-0,3 |
-3 |
9 |
-55,98 |
17,785 |
0,875 |
0,7656 |
| 0,4 |
22,80 |
-0,1 |
-1 |
1 |
-22,80 |
20,647 |
2,153 |
4,6354 |
| 0,6 |
24,97 |
0,1 |
1 |
1 |
24,97 |
23,509 |
1,461 |
2,1345 |
| 0,8 |
26,70 |
0,3 |
3 |
9 |
80,10 |
26,371 |
0,329 |
0,1082 |
| 1,0 |
27,06 |
0,5 |
5 |
25 |
135,30 |
29,233 |
-2,173 |
4,7219 |
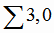 |
132,67 |
0 |
0 |
70 |
100,19 |
|
-0,002 |
19,3510 |
Найдем решение задачи линейной регрессии в кодированных значениях переменной х (4.14). Введем новую переменную по формуле
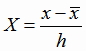 ,
,
где
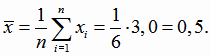
Значения величины
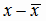 будут целые числа, не имеющие общего множителя, если
принять h = 0,1. Поэтому введем переменную
будут целые числа, не имеющие общего множителя, если
принять h = 0,1. Поэтому введем переменную
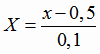 .
.
По формулам (4.15) находим оценки коэффициентов линейной регрессии
 ,
,
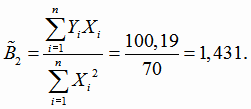
Получили линейную модель регрессии
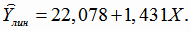 |
(4.32) |
Вычисляем значения линейной модели регрессии
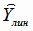 по формуле (4.32) при всех значениях аргумента Х,
а затем рассчитываем
по формуле (4.32) при всех значениях аргумента Х,
а затем рассчитываем 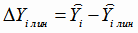 отклонения экспериментальных значений
отклонения экспериментальных значений
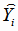 от значений
от значений 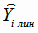 , полученных по функции регрессии. Сумма
, полученных по функции регрессии. Сумма
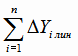 не равна
нулю в силу того, что при вычислении коэффициентов регрессии результаты округлялись с точностью трех знаков после запятой и при вычислении суммы
отклонений набежала ошибка округления. Далее суммируем значения
не равна
нулю в силу того, что при вычислении коэффициентов регрессии результаты округлялись с точностью трех знаков после запятой и при вычислении суммы
отклонений набежала ошибка округления. Далее суммируем значения
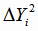 для нахождения дисперсии адекватности
(4.17). Все расчёты приведены в таблице 4.2.
для нахождения дисперсии адекватности
(4.17). Все расчёты приведены в таблице 4.2.
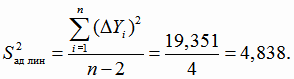
Проверяем адекватность линейной модели регрессии, используя критерий Фишера (4.11).
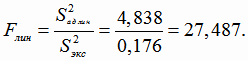
Квантиль распределения Фишера
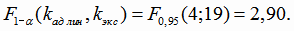 Так как
Так как
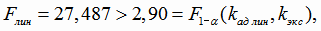
то гипотеза об адекватности линейной модели регрессии отвергается.
Построим квадратичную модель регрессии с кодированной переменной (4.23)
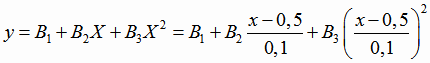 |
(4.33) |
Заметим, что в нашем случае
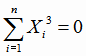 , поэтому для оценок коэффициентов регрессии можно воспользоваться формулами
(4.25). Все расчёты приведены в таблице 4.3.
, поэтому для оценок коэффициентов регрессии можно воспользоваться формулами
(4.25). Все расчёты приведены в таблице 4.3.
Таблица 4.3
Результаты расчёта квадратичной модели регрессии (к задаче 2)
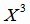 |
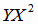
|
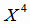 |
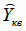 |
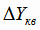 |
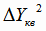 |
| -125 |
307,00 |
626 |
12,558 |
-0,278 |
0,07728 |
| -27 |
167,94 |
81 |
18,258 |
0,402 |
0,16160 |
| -1 |
22,80 |
1 |
22,540 |
0,26 |
0,06760 |
| 1 |
24,97 |
1 |
25,402 |
-0,432 |
0,18662 |
| 27 |
240,30 |
81 |
26,844 |
-0,144 |
0,02074 |
| 125 |
676,50 |
625 |
26,878 |
0,182 |
0,03312 |
| 0 |
1439,51 |
1414 |
|
-0,010 |
0, 54996 |
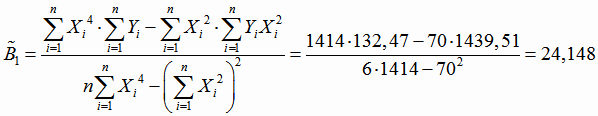 ;
;
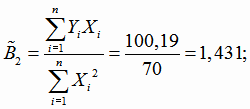
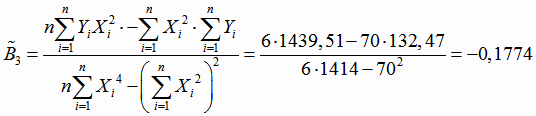 .
.
Получили квадратичную модель регрессии
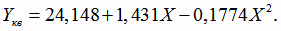 |
(4.34) |
Для расчёта дисперсии адекватности (4.28) вычисляем
 отклонения экспериментальных значений
отклонения экспериментальных значений
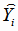 от значений
от значений 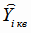 , полученных по функции регрессии. Отличие
, полученных по функции регрессии. Отличие
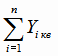 от
нуля объясняется ошибками округления. Проверяем адекватность квадратичной модели регрессии
от
нуля объясняется ошибками округления. Проверяем адекватность квадратичной модели регрессии
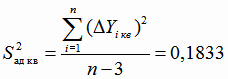 .
.
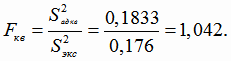
Квантиль распределения Фишера
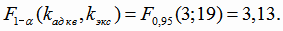 Так как
Так как
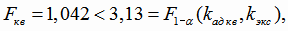
то гипотеза об адекватности квадратичной модели регрессии принимается.
Найдем доверительные интервалы для коэффициентов регрессии. Границы доверительных интервалов (4.27) для коэффициентов В1,
В2 и В3:
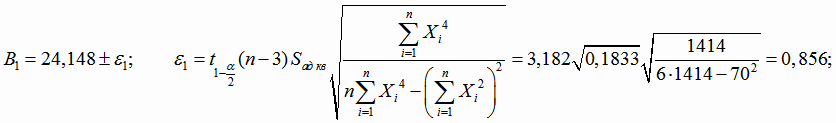
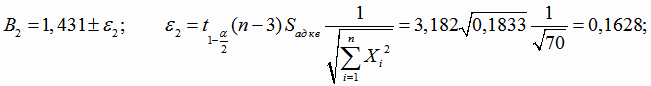
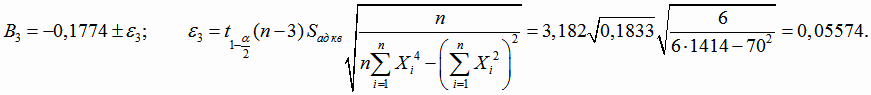
Уравнение квадратичной регрессии Y от исходного переменного х найдем, сделав преобразование:
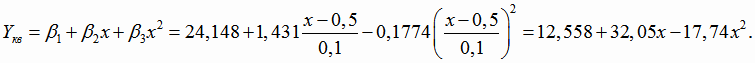
Границы доверительных интервалов для коэффициентов β1, β2 и β3 (4.29):
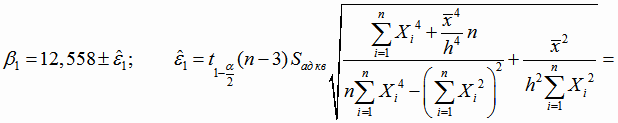
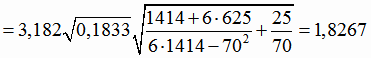 ;
;
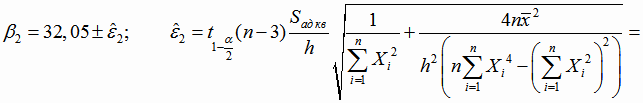
 ;
;
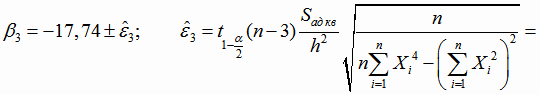
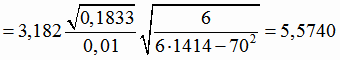 .
.
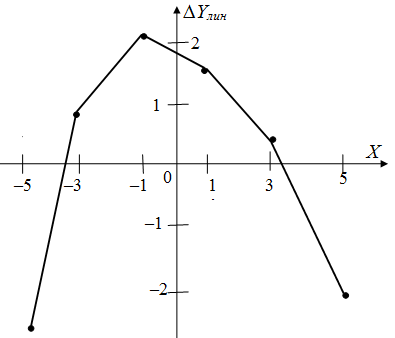
а)
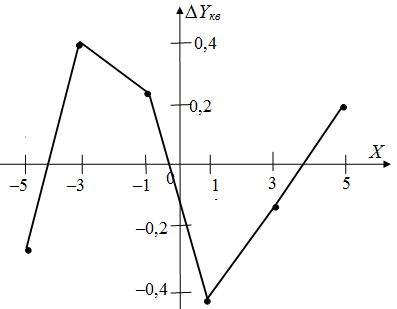
б)
Рис. 4.3. График отклонения экспериментальных данных от линейной модели (а); от квадратичной модели (б).
Для графического анализа результатов расчёта построены графики отклонений линейной и квадратичной моделей регрессии от экспериментальных данных.
На рис. 4.3 а) представлен график отклонений Δ Yлин по приведенной выше таблице 4.2. Из рис. 4.3 а)
видна не только непригодность линейной модели (что следует уже из больших значений отклонений Δ Yлин, явно превышающих
погрешность эксперимента, но и целесообразность расчёта квадратичной модели, так как расположение точек наводит на мысль о параболе.
На рис. 4.3 b) представлен график отклонений Δ Yкв по таблице 4.3, но построенный уже в другом масштабе с увеличением
в 5 раз. Из рис. 4.3 b) видно, что отклонения от параболы, то есть |Δ Yкв| малы (имеют порядок ошибок эксперимента);
это свидетельствует о соответствии квадратичной модели регрессии результатам эксперимента.
Надо также графически сравнить линейную и квадратичную модели с экспериментальными точками. На рис. 4.4 такое сравнение проведено для рассматриваемого
примера; оно показывает соответствие квадратичной модели с экспериментом.
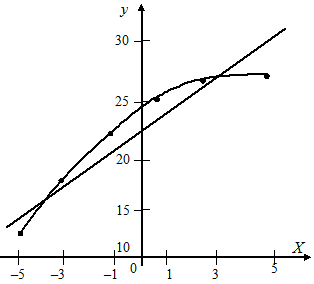
Рис. 4.4. Сравнение линейной и квадратичной моделей с данными эксперимента.
Выводы по работе. По приведенным исходным данным построенная методом наименьших квадратов линейная модель регрессии
неадекватна, квадратичная модель адекватна (уровень значимости α = 0,05).
Уравнение регрессии в кодированных значениях переменной 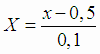 :
:
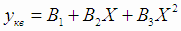
где 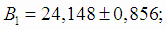
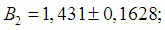
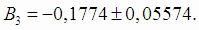
Уравнение регрессии в исходной переменной х:
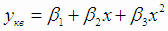 ,
,
где 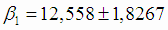 ;
;
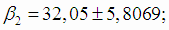
 .
.
Следующая страница
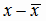
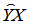
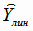
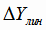
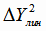
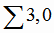
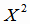
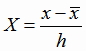 ,
,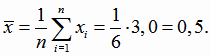
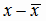 будут целые числа, не имеющие общего множителя, если
принять h = 0,1. Поэтому введем переменную
будут целые числа, не имеющие общего множителя, если
принять h = 0,1. Поэтому введем переменную
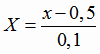 .
. ,
,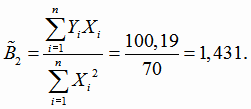
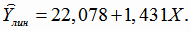
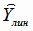 по формуле (4.32) при всех значениях аргумента Х,
а затем рассчитываем
по формуле (4.32) при всех значениях аргумента Х,
а затем рассчитываем 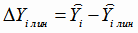 отклонения экспериментальных значений
отклонения экспериментальных значений
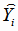 от значений
от значений 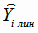 , полученных по функции регрессии. Сумма
, полученных по функции регрессии. Сумма
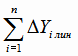 не равна
нулю в силу того, что при вычислении коэффициентов регрессии результаты округлялись с точностью трех знаков после запятой и при вычислении суммы
отклонений набежала ошибка округления. Далее суммируем значения
не равна
нулю в силу того, что при вычислении коэффициентов регрессии результаты округлялись с точностью трех знаков после запятой и при вычислении суммы
отклонений набежала ошибка округления. Далее суммируем значения
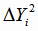 для нахождения дисперсии адекватности
(4.17). Все расчёты приведены в таблице 4.2.
для нахождения дисперсии адекватности
(4.17). Все расчёты приведены в таблице 4.2.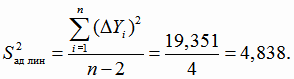
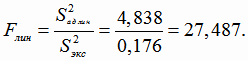
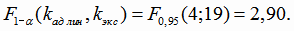 Так как
Так как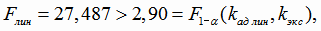
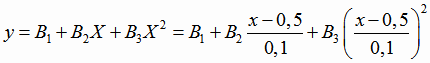
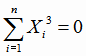 , поэтому для оценок коэффициентов регрессии можно воспользоваться формулами
(4.25). Все расчёты приведены в таблице 4.3.
, поэтому для оценок коэффициентов регрессии можно воспользоваться формулами
(4.25). Все расчёты приведены в таблице 4.3.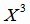
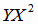
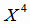
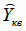
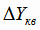
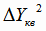
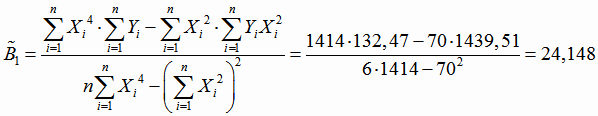 ;
;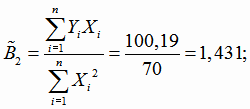
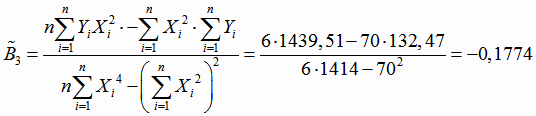 .
.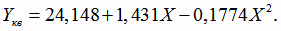
 отклонения экспериментальных значений
отклонения экспериментальных значений
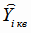 , полученных по функции регрессии. Отличие
, полученных по функции регрессии. Отличие
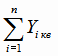 от
нуля объясняется ошибками округления. Проверяем адекватность квадратичной модели регрессии
от
нуля объясняется ошибками округления. Проверяем адекватность квадратичной модели регрессии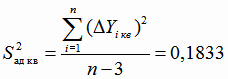 .
.
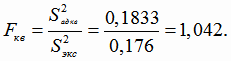
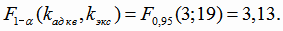 Так как
Так как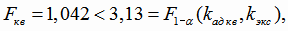
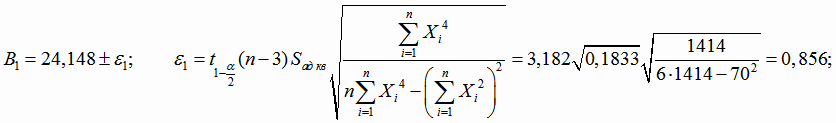
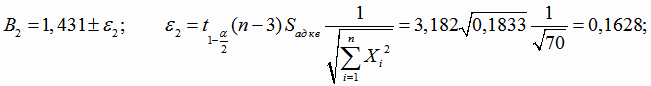
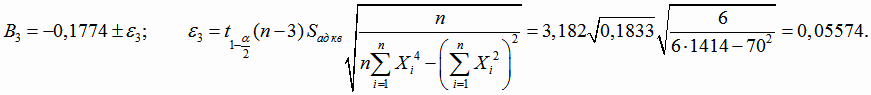
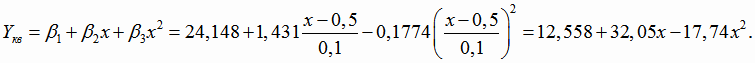
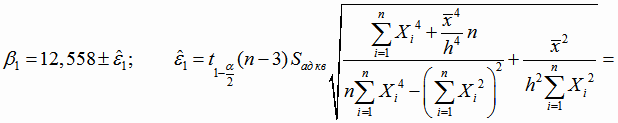
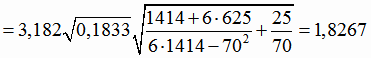 ;
;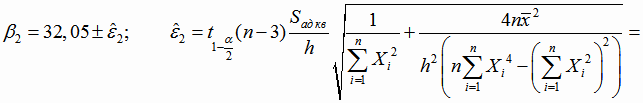
 ;
;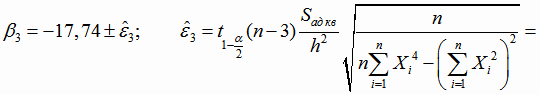
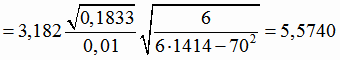 .
.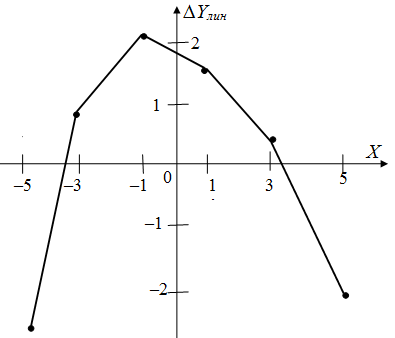
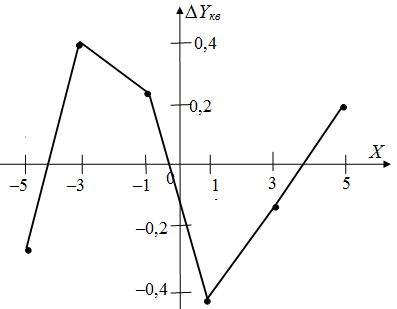
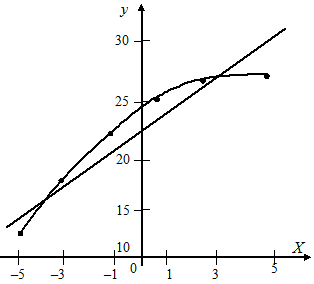
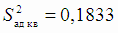
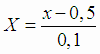 :
: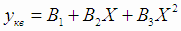
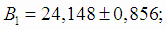
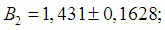
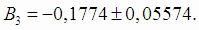
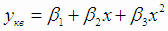 ,
,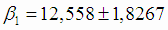 ;
;
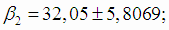
 .
.