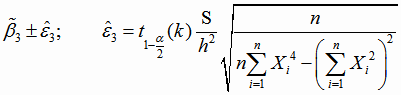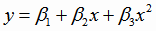,Главная страница Предыдущая страница
1.5 Задача регрессии для квадратичной функции
Рассмотрим случай, когда уравнение регрессии (4.3) является квадратичной функцией
| , |
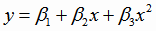(4.21) |
т.е. базисные функции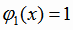 
,
,
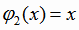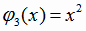. В этом случае система
(4.5) имеет вид
 |
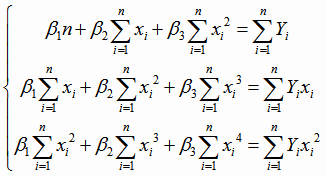(4.22) |
Как и в предыдущем параграфе, сделаем замену
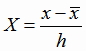, где
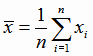- среднее
арифметическое аргументов х, h выбираем из условия, чтобы значения Х были целыми не имеющими общего множителя. Т.е. преобразуем
уравнение (4.21) к виду
 |
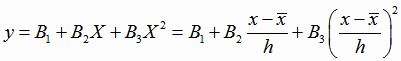(4.23) |
В этом случае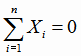 
. Кроме того, введем условие
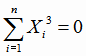. Оно будет
выполняться, например, в том случае, когда переменная х в исходных данных меняется с постоянным шагом. Тогда система (4.22) существенно упрощается:
 |
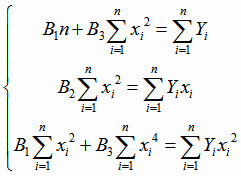(4.24) |
Решая эту систему, получаем формулы для оценок коэффициентов регрессии уравнения с кодированным переменным (4.23):
 ;
 ;
 |
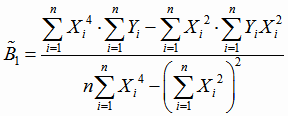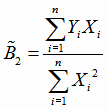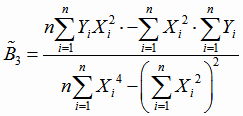(4.25) |
Формула (4.16):
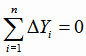для квадратичной модели регрессии также имеет место, и её удобно использовать для
контроля расчётов. Дисперсия адекватности (4.10) для проверки адекватности квадратичной функции регрессии вычисляется по формуле
 |
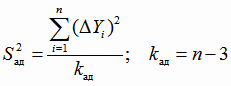(4.26) |
Границы доверительных интервалов для параметров квадратичной функции регрессии с кодированным переменным (4.23) имеют вид
 |
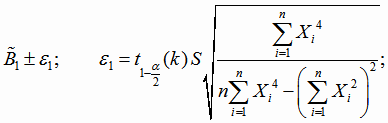
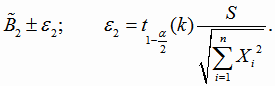(4.27) |
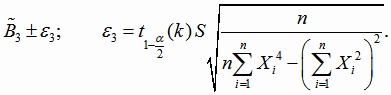
Оценки коэффициентов регрессии квадратичной функции с реальным переменным (4.20) при этом будут
 |
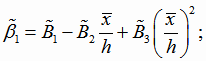
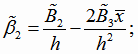
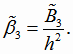(4.28) |
Границы доверительных интервалов для параметров квадратичной функции с реальным переменным (4.20) имеют вид
 |
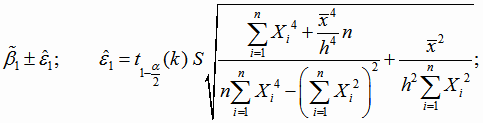
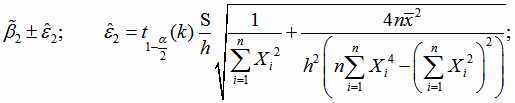(4.29) |
