,Главная страница Предыдущая страница
1.4 Задача регрессии для линейной функции
Рассмотрим случай, когда уравнение регрессии (4.3) является линейной функцией
| , |
(4.12) |
Т.е. базисные функции
,
. В этом случае система (4.5) имеет вид
 |
(4.13) |
Расчёт упростится, если ввести замену 
и рассматривать уравнение
 |
(4.14) |
где 
- среднее арифметическое аргументов х, h выбирается из условия, чтобы значения
Х были целыми не имеющими общего множителя.
Уравнение (4.14) будем называть уравнением с кодированным переменным, в отличие от уравнения (4.12) с реальным переменным.
В этом случае 
и система (4.13) будет иметь вид
Откуда имеем формулы для оценок коэффициентов регрессии уравнения (4.14) с кодированным переменным:
 ,
|
(4.15) |
Для контроля расчётов удобно воспользоваться свойством отклонений
экспериментальных результатов
от рассчитанных по оценкам (4.15) значений функции регрессии
:
 , |
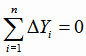(4.16) |
Дисперсия адекватности (4.10) для проверки адекватности линейной регрессионной модели вычисляется по формуле
 |
(4.17) |
Границы доверительных интервалов для параметров линейной функции регрессии с кодированным переменным (4.14) имеют вид
|
(4.18) |
Оценки коэффициентов регрессии линейной функции (4.12) с реальным переменным при этом могут быть найдены по формулам:
 |
(4.19) |
Границы доверительных интервалов для коэффициентов линейной функции с реальным переменным (4.12) имеют вид
 |
(4.20) |
