Главная страница Предыдущая страница
1.3 Проверка гипотезы об адекватности регрессионной модели
Регрессионная модель называется адекватной, если предсказанные по ней значения переменной Y согласуются
с результатами эксперимента. Если модель адекватна, то отклонения результатов эксперимента от полученной функции регрессии 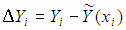 являются реализациями случайных ошибок эксперимента
являются реализациями случайных ошибок эксперимента 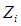 ,которые, в силу предположений (4.1), должны быть независимыми
нормально распределенными случайными величинами с нулевыми средними и одинаковыми дисперсиями
,которые, в силу предположений (4.1), должны быть независимыми
нормально распределенными случайными величинами с нулевыми средними и одинаковыми дисперсиями 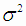 . Проверка выполнения
этих предположений осуществляются статистическими методами и лежит в основе оценки адекватности модели регрессии.
. Проверка выполнения
этих предположений осуществляются статистическими методами и лежит в основе оценки адекватности модели регрессии.
Для проверки адекватности регрессионной модели вычисляют остаточную дисперсию (так называемую дисперсию адекватности) по формуле
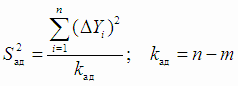 , , |
(4.10) |
где 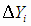 - отклонения средних Yi от проверяемой модели регрессии; kад - число степеней
свободы дисперсии адекватности; n - число точек, в которых проводился эксперимент; m - число оцениваемых параметров
- отклонения средних Yi от проверяемой модели регрессии; kад - число степеней
свободы дисперсии адекватности; n - число точек, в которых проводился эксперимент; m - число оцениваемых параметров 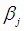 в проверяемой модели.
в проверяемой модели.
Если истинная функция регрессии имеет тот же вид, что и рассматриваемая модель (например, так же, как и модель, представляет
собой квадратичную функцию), то дисперсия адекватности служит несмещенной оценкой истинной дисперсии эксперимента и её можно сравнивать с другими
подобными оценками. В частности, может быть проведена независимая серия измерений для получения оценки дисперсии эксперимента S2экс.
В этом случае S2экс оценивает дисперсию эксперимента Dэкс, 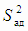 характеризует степень отклонения экспериментальных точек от регрессионной модели, т.е. оценивает некую дисперсию адекватности Dад.
Проверка адекватности модели заключается в проверке гипотезы Н0: Dад = Dэкс при альтернативной
гипотезе Н1: Dад > Dэкс (если модель неадекватна, отклонения экспериментальных точек
от модели будут больше погрешностей эксперимента). Таким образом, задача сводится к проверке гипотезы о равенстве дисперсий, которая решается
с помощью критерия Фишера. Вычисляем отношение
характеризует степень отклонения экспериментальных точек от регрессионной модели, т.е. оценивает некую дисперсию адекватности Dад.
Проверка адекватности модели заключается в проверке гипотезы Н0: Dад = Dэкс при альтернативной
гипотезе Н1: Dад > Dэкс (если модель неадекватна, отклонения экспериментальных точек
от модели будут больше погрешностей эксперимента). Таким образом, задача сводится к проверке гипотезы о равенстве дисперсий, которая решается
с помощью критерия Фишера. Вычисляем отношение
F = 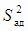 / S2экс / S2экс |
(4.11) |
Если при заданном уровне значимости α отношение F окажется меньше квантили 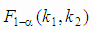 , где
k1 = kад, k2 = kэкс, то рассматриваемая модель не противоречит результатам
эксперимента и принимается; в противоположном случае модель отвергается с уровнем значимости α , как противоречащая результатам эксперимента.
, где
k1 = kад, k2 = kэкс, то рассматриваемая модель не противоречит результатам
эксперимента и принимается; в противоположном случае модель отвергается с уровнем значимости α , как противоречащая результатам эксперимента.
В построенной регрессионной модели (4.3) некоторые коэффициенты могут быть незначимы, т.е. может выполняться гипотеза
Н0: 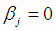 . Для проверки этой гипотезы можно найти доверительный интервал для коэффициента
. Для проверки этой гипотезы можно найти доверительный интервал для коэффициента
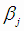 с уровнем значимости α . Если этот интервал “накрывает” значение
с уровнем значимости α . Если этот интервал “накрывает” значение 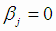 ,
гипотеза Н0 принимается и коэффициент
,
гипотеза Н0 принимается и коэффициент 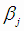 признается незначимым, в противоположном случае
коэффициент
признается незначимым, в противоположном случае
коэффициент 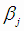 значим.
значим.
Следующая страница
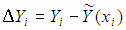 являются реализациями случайных ошибок эксперимента
являются реализациями случайных ошибок эксперимента 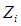 ,которые, в силу предположений (4.1), должны быть независимыми
нормально распределенными случайными величинами с нулевыми средними и одинаковыми дисперсиями
,которые, в силу предположений (4.1), должны быть независимыми
нормально распределенными случайными величинами с нулевыми средними и одинаковыми дисперсиями 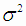 . Проверка выполнения
этих предположений осуществляются статистическими методами и лежит в основе оценки адекватности модели регрессии.
. Проверка выполнения
этих предположений осуществляются статистическими методами и лежит в основе оценки адекватности модели регрессии.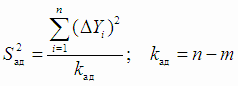 ,
,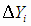 - отклонения средних Yi от проверяемой модели регрессии; kад - число степеней
свободы дисперсии адекватности; n - число точек, в которых проводился эксперимент; m - число оцениваемых параметров
- отклонения средних Yi от проверяемой модели регрессии; kад - число степеней
свободы дисперсии адекватности; n - число точек, в которых проводился эксперимент; m - число оцениваемых параметров 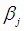 в проверяемой модели.
в проверяемой модели.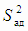 характеризует степень отклонения экспериментальных точек от регрессионной модели, т.е. оценивает некую дисперсию адекватности Dад.
Проверка адекватности модели заключается в проверке гипотезы Н0: Dад = Dэкс при альтернативной
гипотезе Н1: Dад > Dэкс (если модель неадекватна, отклонения экспериментальных точек
от модели будут больше погрешностей эксперимента). Таким образом, задача сводится к проверке гипотезы о равенстве дисперсий, которая решается
с помощью критерия Фишера. Вычисляем отношение
характеризует степень отклонения экспериментальных точек от регрессионной модели, т.е. оценивает некую дисперсию адекватности Dад.
Проверка адекватности модели заключается в проверке гипотезы Н0: Dад = Dэкс при альтернативной
гипотезе Н1: Dад > Dэкс (если модель неадекватна, отклонения экспериментальных точек
от модели будут больше погрешностей эксперимента). Таким образом, задача сводится к проверке гипотезы о равенстве дисперсий, которая решается
с помощью критерия Фишера. Вычисляем отношение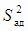 / S2экс
/ S2экс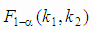 , где
k1 = kад, k2 = kэкс, то рассматриваемая модель не противоречит результатам
эксперимента и принимается; в противоположном случае модель отвергается с уровнем значимости α , как противоречащая результатам эксперимента.
, где
k1 = kад, k2 = kэкс, то рассматриваемая модель не противоречит результатам
эксперимента и принимается; в противоположном случае модель отвергается с уровнем значимости α , как противоречащая результатам эксперимента.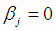 . Для проверки этой гипотезы можно найти доверительный интервал для коэффициента
. Для проверки этой гипотезы можно найти доверительный интервал для коэффициента
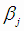 с уровнем значимости α . Если этот интервал “накрывает” значение
с уровнем значимости α . Если этот интервал “накрывает” значение 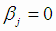 ,
гипотеза Н0 принимается и коэффициент
,
гипотеза Н0 принимается и коэффициент