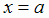 является вертикальной асимптотой графика функции f (х), если выполняется
хотя бы одно из условий:
является вертикальной асимптотой графика функции f (х), если выполняется
хотя бы одно из условий: 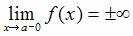 или
или 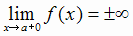 (при этом функция f (х)
может быть вообще не определена соответственно при
(при этом функция f (х)
может быть вообще не определена соответственно при 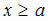 или
или 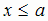 ).
).Главная страница Предыдущая страница
1.3 Асимптоты
Выше было показано, как нахождение точек экстремума и точек перегиба упрощает построение графика и дает возможность установить характерные особенности изменения функции. Во многих случаях построение графика функции облегчается, если предварительно построить асимптоты кривой. Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Прямая 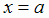 является вертикальной асимптотой графика функции f (х), если выполняется
хотя бы одно из условий:
является вертикальной асимптотой графика функции f (х), если выполняется
хотя бы одно из условий: 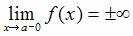 или
или 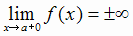 (при этом функция f (х)
может быть вообще не определена соответственно при
(при этом функция f (х)
может быть вообще не определена соответственно при 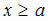 или
или 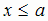 ).
).
Из сказанного следует, что вертикальные асимптоты кривой нужно искать в точках разрыва и на границах области определения.
График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет. Например, график функции 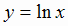 имеет
вертикальную асимптоту х= 0 на границе области определения, так как
имеет
вертикальную асимптоту х= 0 на границе области определения, так как  (см. раздел 1, рис. 1.6).).
(см. раздел 1, рис. 1.6).).
Если 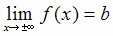 , то
, то 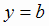 - горизонтальная асимптота кривой у
= f (x) (правая при
- горизонтальная асимптота кривой у
= f (x) (правая при 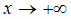 , левая при
, левая при 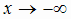 и двусторонняя, если пределы при
и двусторонняя, если пределы при 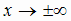 равны).
равны).
Например, график функции 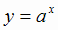 при а > 1 имеет левую горизонтальную асимптоту у =
0, так как
при а > 1 имеет левую горизонтальную асимптоту у =
0, так как 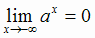 . Правой горизонтальной асимптоты у кривой нет, поскольку
. Правой горизонтальной асимптоты у кривой нет, поскольку 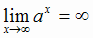 (см. раздел 1, рис. 1.5).
(см. раздел 1, рис. 1.5).
Прямая 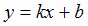 называется наклонной асимптотой графика функции у = f (x), если
называется наклонной асимптотой графика функции у = f (x), если
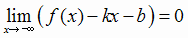 (левая наклонная асимптота) или
(левая наклонная асимптота) или  (правая наклонная асимптота).
(правая наклонная асимптота).
Существование наклонной асимптоты определяется следующим условием. Для того чтобы кривая у = f (x) имела
асимптоту 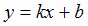 , необходимо и достаточно, чтобы существовали конечные пределы
, необходимо и достаточно, чтобы существовали конечные пределы
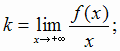 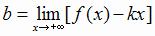 |
(2.1) |
или
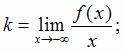 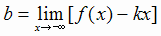 |
(2.2) |
В первом случае получается правая наклонная асимптота, во втором - левая. Правая наклонная асимптота изображена на рис. 2.9.
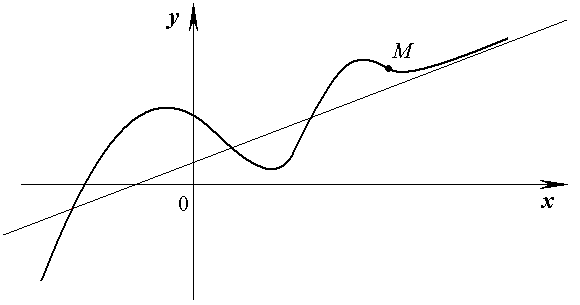
Рис. 2.9.
При совпадении пределов (2.1) и (2.2) прямая у = kx + b является двусторонней асимптотой кривой. Если хотя бы один
из пределов, определяющих асимптоту 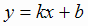 , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота у = b является частным случаем наклонной у = kx + b при k = 0. Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример. Найдем асимптоты графика функции 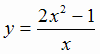 и построим эскиз графика.
и построим эскиз графика.
Решение. Функции определена на всей числовой прямой, кроме 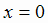 , т.е.
, т.е. 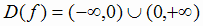 ,
Поэтому в точке разрыва
,
Поэтому в точке разрыва 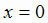 кривая может иметь вертикальную асимптоту. Действительно,
кривая может иметь вертикальную асимптоту. Действительно,
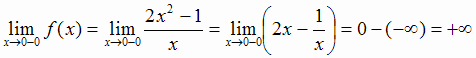
Аналогично,

Следовательно, х = 0 - вертикальная асимптота; при 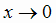 слева
слева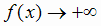 , при
, при
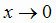 справа
справа 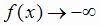 .
.
Горизонтальной асимптоты кривая не имеет, так как
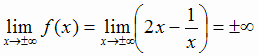
Выясним наличие наклонной асимптоты:
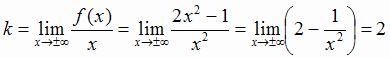 ;
;
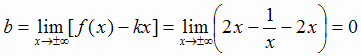
Прямая  является двусторонней наклонной асимптотой заданной кривой (рис. 2.10).
является двусторонней наклонной асимптотой заданной кривой (рис. 2.10).

Рис. 2.10.