Главная страница Предыдущая страница
1.2 Направление выпуклости графика функции. Точки перегиба
Пусть функция f(x) дифференцируема на интервале (a; b), тогда в любой точке 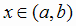 существует касательная к графику этой функции. График дифференцируемой функции называется выпуклым вверх в интервале
существует касательная к графику этой функции. График дифференцируемой функции называется выпуклым вверх в интервале  если в этом интервале он расположен ниже любой своей касательной (рис. 2.5). График дифференцируемой функции называется, выпуклым вниз в
интервале
если в этом интервале он расположен ниже любой своей касательной (рис. 2.5). График дифференцируемой функции называется, выпуклым вниз в
интервале  , если в этом интервале он расположен выше любой своей касательной (рис. 2.6).
, если в этом интервале он расположен выше любой своей касательной (рис. 2.6).
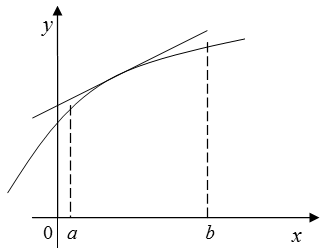
Рис. 2.5.
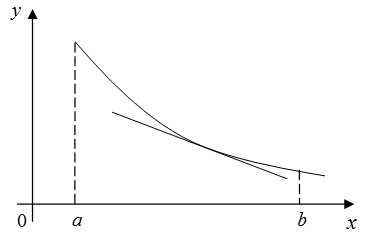
Рис. 2.6.
Теорема. Достаточный признак направления выпуклости графика функции. Если для функции f (х) во всех
точках интервала 
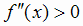 , то кривая у=f(х) выпукла вниз в этом интервале; если
же
, то кривая у=f(х) выпукла вниз в этом интервале; если
же 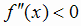 во всех точках интервала
во всех точках интервала  , то кривая выпукла вверх в этом интервале.
, то кривая выпукла вверх в этом интервале.
Точка  графика непрерывной функции, в которой изменяется направление выпуклости,
называется точкой перегиба графика функции, а x0 называется точкой перегиба функции.
графика непрерывной функции, в которой изменяется направление выпуклости,
называется точкой перегиба графика функции, а x0 называется точкой перегиба функции.
Из определения следует, что с одной стороны от точки перегиба кривая расположена под касательной, с другой стороны - над
ней, или наоборот. Поэтому точку перегиба на графике принято показывать отрезком касательной, которая в этой точке пересекает кривую (рис. 2.7).
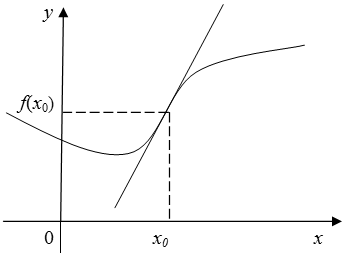
Рис. 2.7.
Теорема. Достаточный признак существования точки перегиба. Если в точке x0 функция f (х)
имеет первую производную 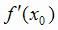 , а вторая производная
, а вторая производная 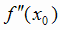 в этой точке равна нулю или не существует
и, кроме того,
в этой точке равна нулю или не существует
и, кроме того, 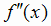 при переходе через x0 меняет знак, то
при переходе через x0 меняет знак, то 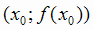 является точкой
перегиба графика функции
является точкой
перегиба графика функции 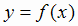 .
.
Таким образом, чтобы исследовать характер выпуклости кривой у = f (х), нужно найти те точки, в которых 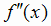 =
0 или
=
0 или 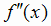 не существует, а затем, используя достаточный признак, исследовать знаки второй производной слева и справа
от каждой возможной точки перегиба (подобно тому, как определялись точки экстремума по первой производной).
не существует, а затем, используя достаточный признак, исследовать знаки второй производной слева и справа
от каждой возможной точки перегиба (подобно тому, как определялись точки экстремума по первой производной).
Пример. Найдем точки перегиба и построим график функции 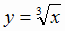 .
.
Решение. Функция определена при 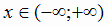 . Её производные
. Её производные 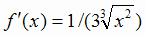 и
и 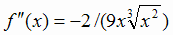 . Здесь
. Здесь 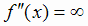 при
при 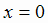 , причем
, причем 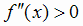 при х < 0 и
при х < 0 и 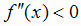 при х > 0. Следовательно, слева от х = 0 кривая выпукла вниз, а справа - выпукла
вверх, т. е. О(0; 0) - точка перегиба графика. В этой точке угловой коэффициент касательной
при х > 0. Следовательно, слева от х = 0 кривая выпукла вниз, а справа - выпукла
вверх, т. е. О(0; 0) - точка перегиба графика. В этой точке угловой коэффициент касательной 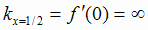 , поэтому касательная
вертикальна (рис. 2.8).
, поэтому касательная
вертикальна (рис. 2.8).
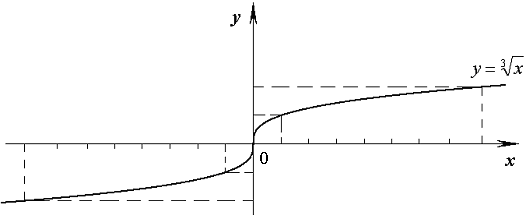
Рис. 2.8.
Следующая страница
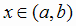 существует касательная к графику этой функции. График дифференцируемой функции называется выпуклым вверх в интервале
существует касательная к графику этой функции. График дифференцируемой функции называется выпуклым вверх в интервале  если в этом интервале он расположен ниже любой своей касательной (рис. 2.5). График дифференцируемой функции называется, выпуклым вниз в
интервале
если в этом интервале он расположен ниже любой своей касательной (рис. 2.5). График дифференцируемой функции называется, выпуклым вниз в
интервале  , если в этом интервале он расположен выше любой своей касательной (рис. 2.6).
, если в этом интервале он расположен выше любой своей касательной (рис. 2.6).

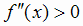 , то кривая у=f(х) выпукла вниз в этом интервале; если
же
, то кривая у=f(х) выпукла вниз в этом интервале; если
же 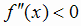 во всех точках интервала
во всех точках интервала  графика непрерывной функции, в которой изменяется направление выпуклости,
называется точкой перегиба графика функции, а x0 называется точкой перегиба функции.
графика непрерывной функции, в которой изменяется направление выпуклости,
называется точкой перегиба графика функции, а x0 называется точкой перегиба функции.
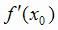 , а вторая производная
, а вторая производная 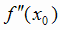 в этой точке равна нулю или не существует
и, кроме того,
в этой точке равна нулю или не существует
и, кроме того, 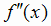 при переходе через x0 меняет знак, то
при переходе через x0 меняет знак, то 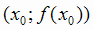 является точкой
перегиба графика функции
является точкой
перегиба графика функции 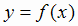 .
.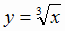 .
.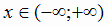 . Её производные
. Её производные 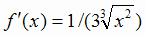 и
и 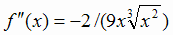 . Здесь
. Здесь 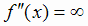 при
при 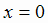 , причем
, причем 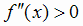 при х < 0 и
при х < 0 и 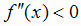 при х > 0. Следовательно, слева от х = 0 кривая выпукла вниз, а справа - выпукла
вверх, т. е. О(0; 0) - точка перегиба графика. В этой точке угловой коэффициент касательной
при х > 0. Следовательно, слева от х = 0 кривая выпукла вниз, а справа - выпукла
вверх, т. е. О(0; 0) - точка перегиба графика. В этой точке угловой коэффициент касательной 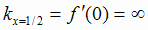 , поэтому касательная
вертикальна (рис. 2.8).
, поэтому касательная
вертикальна (рис. 2.8).