
1 Теоретическое введение
1.1 Экстремумы функции. Признаки возрастания и убывания функции
Рассмотрим график непрерывной функции. Из рис. 2.1 видно, что значение функции в точке x1 меньше, чем значения функции в достаточно близких к ней точках, соседних с ней справа и слева. В этом случае говорят, что функция имеет в точке x1, минимум.

Рис. 2.1
Точка x0 называется точкой локального минимума функции f (х), если f (х)
непрерывна в точке x0 и существует такая окрестность точки x0, что для всех 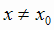 из
этой окрестности выполняется неравенство
из
этой окрестности выполняется неравенство 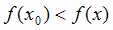 . При этом говорят, что функция f (х) имеет минимум
в точке x0.
. При этом говорят, что функция f (х) имеет минимум
в точке x0.
В точке x2 (рис. 2.1) значение функции больше значений функции в достаточно близких к ней точках, расположенных справа и слева от нее. В этом случае говорят, что функция имеет в точке x2 максимум.
Непрерывная в точке x0 функция f (х) имеет максимум в точке x0,
если существует такая окрестность точки x0, что для всех 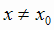 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство
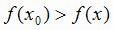 , при этом точка x0 называется точкой максимума функции f (х).
, при этом точка x0 называется точкой максимума функции f (х).
Для точек максимума и минимума существует объединяющий их термин - точки экстремума, а значения функции этих точках называются экстремумами функции.
Из приведенных определений следует, что экстремум функции имеет локальный характер - это наибольшее или наименьшее значение функции по сравнению с близлежащими значениями. На промежутке функция может иметь несколько экстремумов, причем может оказаться, что какой-либо минимум функции больше какого-либо максимума. Следующая теорема позволяет ответить на вопрос, в каких точках функция может достигать экстремума.
Теорема Ферма (необходимый признак экстремума). Если функция f(x) дифференцируема в точке x0
и имеет в этой точке экстремум, то её производная при 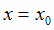 обращается в нуль, т.е.
обращается в нуль, т.е.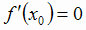 .
.
Теорема Ферма имеет простое геометрическое истолкование. Так как производная в точке x0 равна угловому
коэффициенту касательной к графику функции в этой точке, то равенство 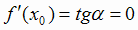 означает, что
означает, что 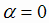 , т.
е. касательная к кривой в точке экстремума дифференцируемой функции параллельна оси Ох (рис. 2.1).
, т.
е. касательная к кривой в точке экстремума дифференцируемой функции параллельна оси Ох (рис. 2.1).
Таким образом, дифференцируемая функция может иметь экстремум лишь в тех точках, где производная равна нулю. Однако функция
может иметь экстремум и в тех точках области определения, где производная не существует. Например, функция 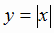 в точке
в точке 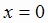 достигает минимума, но не дифференцируема при
достигает минимума, но не дифференцируема при 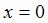 (см. раздел 1, рис. 1.17). Функция,
изображенная на рис. 1.2, имеет в точке x0 максимум, но не дифференцируема в этой точке. так как при
(см. раздел 1, рис. 1.17). Функция,
изображенная на рис. 1.2, имеет в точке x0 максимум, но не дифференцируема в этой точке. так как при 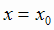 касательная к кривой образует с осью Ох угол 90° (
касательная к кривой образует с осью Ох угол 90° (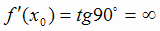 ).
).
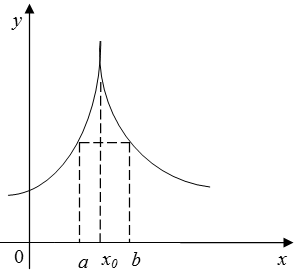
Рис. 1.2.
Условия 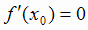 и
и 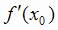 не существует являются необходимыми условиями экстремума,
но не достаточными, поскольку можно привести примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция
не имеет. Например, функция
не существует являются необходимыми условиями экстремума,
но не достаточными, поскольку можно привести примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция
не имеет. Например, функция 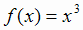 имеет производную
имеет производную 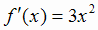 , которая обращается в нуль при х =
0, однако в точке
, которая обращается в нуль при х =
0, однако в точке 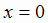 функции экстремума не имеет (см. раздел 1, рис. 1.1).
функции экстремума не имеет (см. раздел 1, рис. 1.1).
Те значения аргумента, при которых функция f (x) сохраняет непрерывность, а её производная 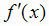 обращается в нуль или не существует, называются критическими точками (или критическими значениями аргумента).
обращается в нуль или не существует, называются критическими точками (или критическими значениями аргумента).
Если во всех точках некоторого промежутка 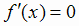 , то функция f(x) сохраняет в этом промежутке
постоянное значение. Если во всех точках некоторого промежутка
, то функция f(x) сохраняет в этом промежутке
постоянное значение. Если во всех точках некоторого промежутка 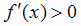 , то функция f (х) возрастает
в этом промежутке (достаточный признак возрастания). Если во всех точках некоторого промежутка
, то функция f (х) возрастает
в этом промежутке (достаточный признак возрастания). Если во всех точках некоторого промежутка 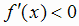 , то f(x)
убывает на этом промежутке (достаточный признак убывания).
, то f(x)
убывает на этом промежутке (достаточный признак убывания).
Из вышеизложенного следует, что экстремум функции может достигаться только в критических точках, т. е. в тех точках, в
которых f (х) непрерывна, 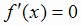 , либо
, либо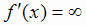 , либо
, либо 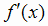 не существует.
Но это является лишь необходимым признаком экстремума, так как не в каждой критической точке экстремум существует. Поэтому нужно располагать
достаточными признаками, позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно, максимум или минимум.
не существует.
Но это является лишь необходимым признаком экстремума, так как не в каждой критической точке экстремум существует. Поэтому нужно располагать
достаточными признаками, позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно, максимум или минимум.
Теорема (первый достаточный признак экстремума). Если x0 - критическая точка функции f (х)
и в некоторой окрестности этой точки, слева и справа от нее, производная имеет противоположные знаки, то 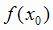 является
экстремумом функции, причем:
является
экстремумом функции, причем:
1) максимумом, если 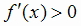 при
при 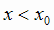 и
и 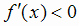 при
при 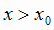 ;
;
2) минимумом, если 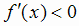 при
при 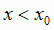 и
и 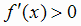 при
при 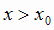 .
.
Таким образом, если x0 - критическая точка f (х) и при переходе через x0
производная 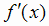 меняет знак, то x0 есть точка экстремума, причем точка максимума, если производная меняет
знак с плюса на минус, и точка минимума, если - с минуса на плюс. В противном случае в точке x0 экстремума нет.
меняет знак, то x0 есть точка экстремума, причем точка максимума, если производная меняет
знак с плюса на минус, и точка минимума, если - с минуса на плюс. В противном случае в точке x0 экстремума нет.
Теперь нетрудно сделать практические выводы. Пусть речь идет об отыскании экстремумов функции, непрерывной в некотором
промежутке и имеющей в нём конечное множество критических точек. Отыскав все критические точки, нужно расположить их в порядке возрастания:
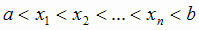 , где а и b - концы промежутка. Так как все точки, в которых
, где а и b - концы промежутка. Так как все точки, в которых 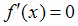 или
или 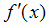 не существует, входят в число точек
не существует, входят в число точек  то в каждом из интервалов
то в каждом из интервалов 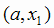
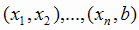 существует производная
существует производная 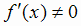 , которая внутри интервала сохраняет знак (функция внутри интервала монотонна). Поэтому, чтобы
установить знак производной в указанных интервалах, достаточно взять в каждом интервале по одной контрольной точке и установить знак производной
в этой точке.
, которая внутри интервала сохраняет знак (функция внутри интервала монотонна). Поэтому, чтобы
установить знак производной в указанных интервалах, достаточно взять в каждом интервале по одной контрольной точке и установить знак производной
в этой точке.
Последовательности интервалов монотонности функции соответствует некоторая последовательность плюсов и минусов, характер чередования которых на основании первого достаточного признака экстремума позволит судить о наличии максимума, минимума или об отсутствии экстремума в соответствующей точке.
Пример. Исследуем на экстремум функцию 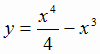 и построим её график.
и построим её график.
Решение. Функция определена и непрерывна на всей числовой прямой, т. е. 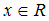 . Её производная
. Её производная
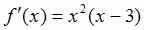 существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых
существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых 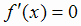 ,
т. е.
,
т. е. 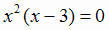 , откуда
, откуда 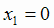 и
и 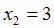 . Критические точки
. Критические точки 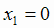 и
и
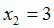 разбивают всю область определения функции на три интервала монотонности:
разбивают всю область определения функции на три интервала монотонности: 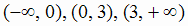 . Выберем в каждом
из них по одной контрольной точке и найдем знак производной в этой точке.
. Выберем в каждом
из них по одной контрольной точке и найдем знак производной в этой точке.
Для интервала 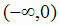 контрольной точкой может служить
контрольной точкой может служить 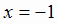 ; находим
; находим 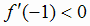 .
Взяв в интервале (0, 3) точку х = 1, получим
.
Взяв в интервале (0, 3) точку х = 1, получим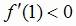 , а взяв в интервале (0, 3) точку х = 4, имеем
, а взяв в интервале (0, 3) точку х = 4, имеем 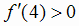 .
Итак, в интервалах
.
Итак, в интервалах 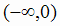 и (0, 3)
и (0, 3) 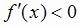 , а в интервале
, а в интервале 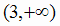
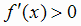 .
Согласно первому достаточному признаку экстремума, в точке х = 0 экстремума нет (так как производная сохраняет знак в интервале
.
Согласно первому достаточному признаку экстремума, в точке х = 0 экстремума нет (так как производная сохраняет знак в интервале 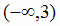 ),
а в точке х = 3 функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдем соответствующие
значения функции:
),
а в точке х = 3 функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдем соответствующие
значения функции: 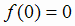 ,
, 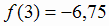 . В интервале
. В интервале 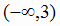 функция убывает, так как в этом
интервале
функция убывает, так как в этом
интервале 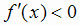 , а в интервале
, а в интервале 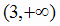 - возрастает, так как в этом интервале
- возрастает, так как в этом интервале 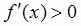 .
.
Чтобы уточнить построение графика, найдем точки пересечения его с осями координат. При у = 0 получим уравнение
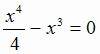 , корни которого
, корни которого 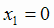 и
и 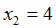 , т. е. найдены две точки (0;
0) и (4; 0) графика функции. Используя все полученные сведения, строим график (рис. 2.3). Заметим, что из условия
, т. е. найдены две точки (0;
0) и (4; 0) графика функции. Используя все полученные сведения, строим график (рис. 2.3). Заметим, что из условия 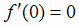 следует, что касательная к графику функции при х = 0 горизонтальна, т.е. в точке (0; 0) ось Ох является касательной к графику функции.
следует, что касательная к графику функции при х = 0 горизонтальна, т.е. в точке (0; 0) ось Ох является касательной к графику функции.
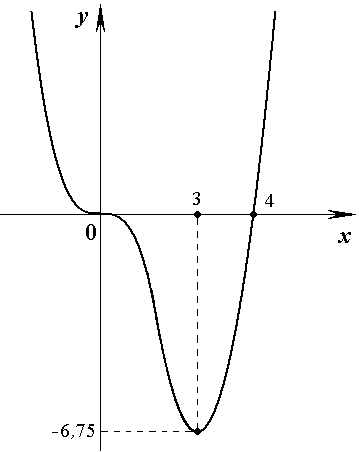
Рис. 2.3.
Исследование на экстремум может выполняться и с помощью второй производной.
Теорема. (Второй достаточный признак экстремума). Если функция f (х) дважды дифференцируема
в окрестности точки x0, 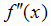 непрерывна в точке x0 и в точке x0 выполняются
условия:
непрерывна в точке x0 и в точке x0 выполняются
условия: 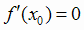 ,
, 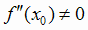 , то в этой точке функция имеет экстремум, причем максимум, если
, то в этой точке функция имеет экстремум, причем максимум, если 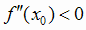 ,
и минимум, если
,
и минимум, если 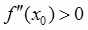 .
.
Пример. Исследовать на экстремум функцию 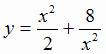 и построить её график.
и построить её график.
Решение. Областью определения функции является числовая прямая кроме точки х = 0, т.е. 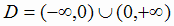 .
.
Для сокращения исследования можно воспользоваться тем, что данная функция четная, так как 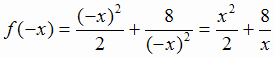 .
Поэтому её график симметричен относительно оси Оу и исследование можно выполнить только для интервала
.
Поэтому её график симметричен относительно оси Оу и исследование можно выполнить только для интервала 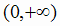
Находим производную 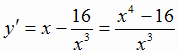 и критические точки функции:
и критические точки функции:
1) 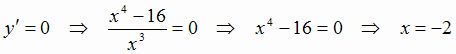 и
и 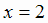 ;
;
2) 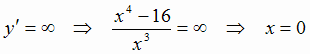 ,
,
но функция терпит разрыв в этой точке, поэтому она не может быть точкой экстремума.
Таким образом, заданная функция имеет две критические точки: 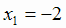 и
и 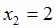 . Учитывая
четность функции, проверим по второму достаточному признаку экстремума только точку
. Учитывая
четность функции, проверим по второму достаточному признаку экстремума только точку 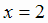 . Для этого найдем вторую производную
. Для этого найдем вторую производную
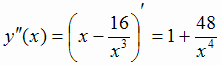 и определим её знак при
и определим её знак при 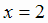 ; получим
; получим 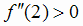 . Так как f
(2) = 0 и
. Так как f
(2) = 0 и 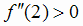 , то х = 2 является точкой минимума функции; при этом
, то х = 2 является точкой минимума функции; при этом 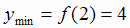 .
.
Чтобы составить более полное представление о графике функции, выясним её поведение на границах области определения:
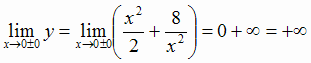
(здесь символом 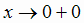 обозначено стремление х к нулю справа, причем х остается положительным; аналогично,
обозначено стремление х к нулю справа, причем х остается положительным; аналогично,
 означает стремление х к нулю слева, причем х остается отрицательным). Таким образом, если
означает стремление х к нулю слева, причем х остается отрицательным). Таким образом, если 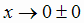 ,
то
,
то 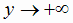 . Далее, находим
. Далее, находим
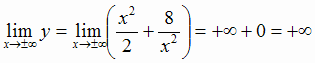 ,
,
т.е. если 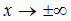 то
то 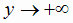 .
.
Точек пересечения с осями график функции не имеет. Он изображен на рис. 2.4.
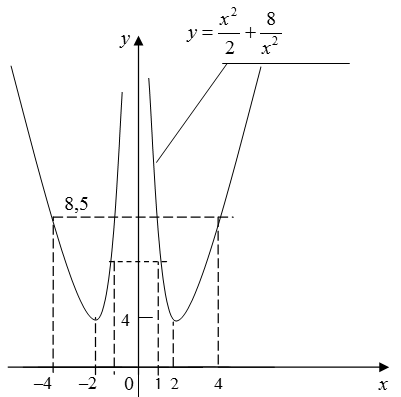
Рис. 2.4.