 и
и 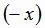 , если
, если 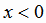 , т.е.
, т.е.Главная страница Предыдущая страница
1.4 Модуль действительного числа. Построение графиков функций с модулем
Абсолютной величиной или модулем действительного числа х называется само это число, если  и
и 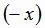 , если
, если 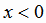 , т.е.
, т.е.
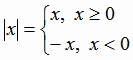 |
(1.4) |
График функции 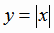 приведен на рис. 1.17.
приведен на рис. 1.17.
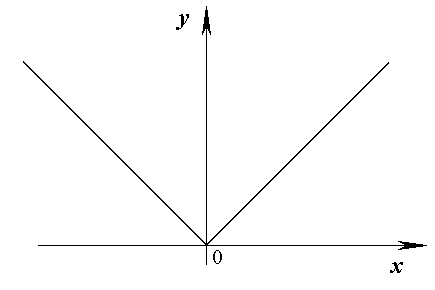
Рис. 1.17
Отметим следующие свойства модуля, справедливые для любых действительных х и y:
1) Модуль произведения равен произведению модулей:
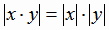 |
(1.5) |
2) Модуль частного является частным модулей:
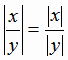 |
(1.6) |
3) Корень квадратный из х в квадрате равен модулю числа х:
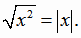 |
(1.7) |
Если известен график функции 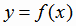 , график функции
, график функции 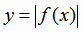 можно
построить согласно определению модуля (1.4). Действительно,
можно
построить согласно определению модуля (1.4). Действительно,
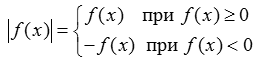
Поэтому, для построения графика функции 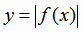 построим сначала график функции
построим сначала график функции 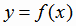 (рис. 1.18). Затем часть графика, где у принимает неотрицательные значения, оставим без изменения. А ту часть графика, где у принимает
отрицательные значения, зеркально отразим относительно оси абсцисс, т. е. умножим соответствующие значения у на минус единицу. Мы получили
график функции
(рис. 1.18). Затем часть графика, где у принимает неотрицательные значения, оставим без изменения. А ту часть графика, где у принимает
отрицательные значения, зеркально отразим относительно оси абсцисс, т. е. умножим соответствующие значения у на минус единицу. Мы получили
график функции 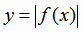 (рис. 1.19).
(рис. 1.19).
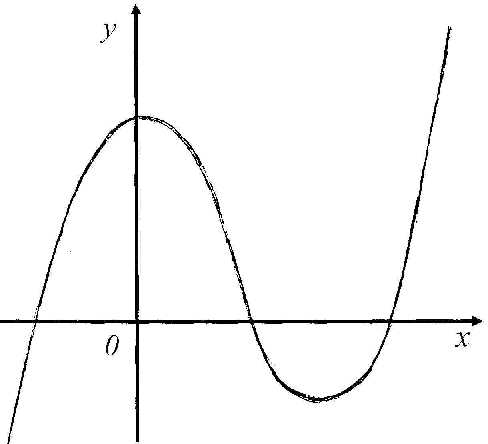
Рис. 1.18.
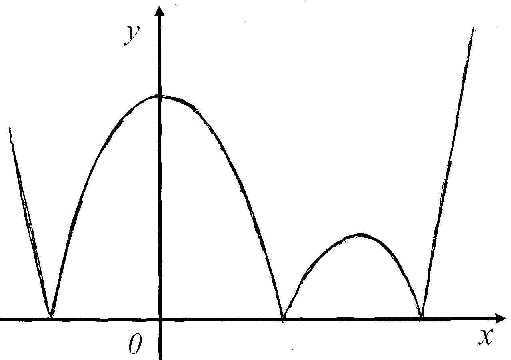
Рис. 1.19