Главная страница Предыдущая страница
1.3 Обратные функции
Пусть функция 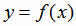 определена на множестве Х и имеет множество значений Y. Пусть эта
функция определяет взаимно однозначное соответствие между множествами Х и Y, т.е.
определена на множестве Х и имеет множество значений Y. Пусть эта
функция определяет взаимно однозначное соответствие между множествами Х и Y, т.е. 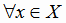 соответствует
единственное значение
соответствует
единственное значение 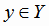 и, наоборот,
и, наоборот, 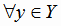 соответствует единственное значение
соответствует единственное значение 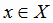 .
Тогда для каждого
.
Тогда для каждого 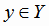 существует единственное значение х такое, что
существует единственное значение х такое, что 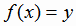 , и это соответствие
определяет функцию, называемую обратной по отношению к данной функции
, и это соответствие
определяет функцию, называемую обратной по отношению к данной функции 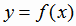 и обозначаемую
и обозначаемую 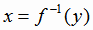 .
.
Функция 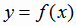 и её обратная функция
и её обратная функция 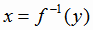 выражает одну и ту же связь между переменными
х и у. Но в первом случае мы рассматриваем х как независимую переменную, а у как функцию; во втором случае - наоборот:
у мы считаем независимой переменной, а х - функцией. График обратной функции
выражает одну и ту же связь между переменными
х и у. Но в первом случае мы рассматриваем х как независимую переменную, а у как функцию; во втором случае - наоборот:
у мы считаем независимой переменной, а х - функцией. График обратной функции 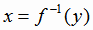 совпадает с графиком функции
совпадает с графиком функции
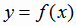 , если значения независимой переменной обратной функции у откладывать на оси Оу. Если же обратную функцию
представить в виде
, если значения независимой переменной обратной функции у откладывать на оси Оу. Если же обратную функцию
представить в виде 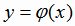 , т.е. независимую переменную обозначить х, значение функции - у и значения независимой
переменной откладывать на оси Ох, то график обратной функции будет симметричен графику функции
, т.е. независимую переменную обозначить х, значение функции - у и значения независимой
переменной откладывать на оси Ох, то график обратной функции будет симметричен графику функции 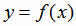 относительно
биссектрисы первого и третьего координатных углов, имеющей уравнение
относительно
биссектрисы первого и третьего координатных углов, имеющей уравнение 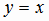 . При этом область значений функции
. При этом область значений функции 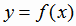 становится областью определения обратной функции
становится областью определения обратной функции 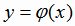 , а область определения функции
, а область определения функции 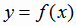 - областью
значений обратной функции.
- областью
значений обратной функции.
Заметим, что некоторые функции не имеют обратных. Например, функция 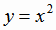 , если её рассматривать на
всей числовой оси, не имеет обратной функции, так как каждому значению
, если её рассматривать на
всей числовой оси, не имеет обратной функции, так как каждому значению 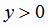 соответствует два значения
соответствует два значения 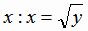 и
и 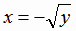 (рис.1.11). Если же функцию
(рис.1.11). Если же функцию 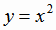 рассматривать на промежутке
рассматривать на промежутке 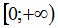 ,
то она имеет обратную функцию
,
то она имеет обратную функцию 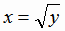 , так как на этом интервале каждому значению у соответствует единственное
значение х (рис. 1.11).
, так как на этом интервале каждому значению у соответствует единственное
значение х (рис. 1.11).
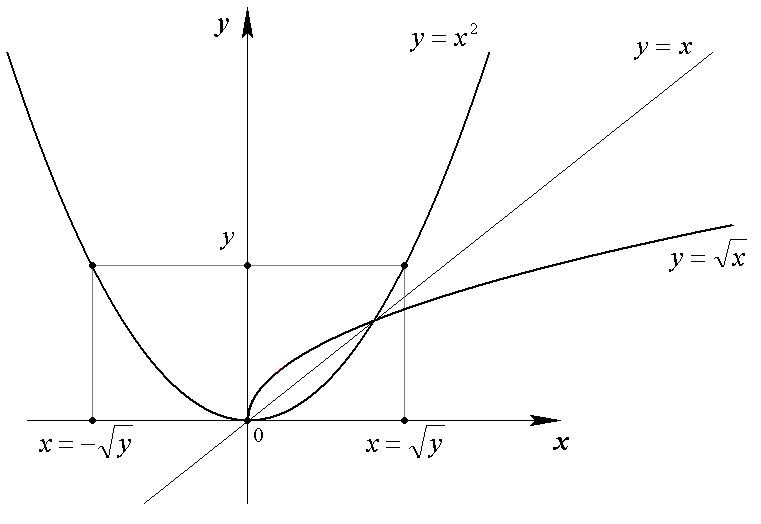
Рис. 1.11
Возникает вопрос, какова должна быть функция 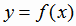 , чтобы она имела обратную. Прежде чем ответить на
этот вопрос, введем понятия возрастающей и убывающей функции. Пусть функция
, чтобы она имела обратную. Прежде чем ответить на
этот вопрос, введем понятия возрастающей и убывающей функции. Пусть функция 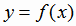 определена на множестве Х.
определена на множестве Х.
Функция 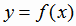 называется возрастающей на множестве Х, если для любых
называется возрастающей на множестве Х, если для любых 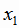 и
и 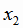 , принадлежащих Х, из условия
, принадлежащих Х, из условия 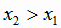 следует
следует 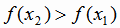 , т.е. большему значению
аргумента соответствует большее значение функции.
, т.е. большему значению
аргумента соответствует большее значение функции.
Функция 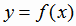 называется убывающей на множестве Х, если для любых
называется убывающей на множестве Х, если для любых 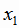 и
и 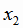 , принадлежащих Х, из условия
, принадлежащих Х, из условия 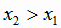 следует
следует 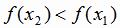 , т.е. большему значению
аргумента соответствует меньшее значение функции.
, т.е. большему значению
аргумента соответствует меньшее значение функции.
На рис. 1.12 приведены графики возрастающей и убывающей функций. Например, функция 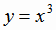 является возрастающей
на всей числовой оси; функция
является возрастающей
на всей числовой оси; функция 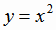 возрастает на промежутке
возрастает на промежутке 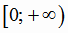 и убывает на промежутке
и убывает на промежутке
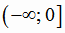 .
.

Рис. 1.12
Если функция 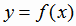 , заданная на множестве Х, является только возрастающей или только убывающей
на этом множестве, то она называется строго монотонной на множестве Х.
, заданная на множестве Х, является только возрастающей или только убывающей
на этом множестве, то она называется строго монотонной на множестве Х.
Из рис. 1.12 непосредственно видно, что строго монотонная функция 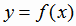 осуществляет взаимно однозначное
соответствие между областью определения и множеством значений функции, т.е. каждому значению у соответствует единственное значение х,
и, следовательно, функция
осуществляет взаимно однозначное
соответствие между областью определения и множеством значений функции, т.е. каждому значению у соответствует единственное значение х,
и, следовательно, функция 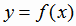 имеет обратную. Таким образом, достаточным условием существования обратной функции на
множестве Х является монотонность функции
имеет обратную. Таким образом, достаточным условием существования обратной функции на
множестве Х является монотонность функции 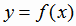 на этом множестве.
на этом множестве.
Показательная функция 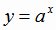 является строго монотонной на всей области определения. Если
является строго монотонной на всей области определения. Если 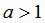 ,
то функция
,
то функция 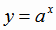 возрастающая, если
возрастающая, если 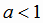 - убывающая (рис. 1.5). Поэтому на всей области определения
показательная функция имеет обратную. Обратной к показательной функции является логарифмическая функция
- убывающая (рис. 1.5). Поэтому на всей области определения
показательная функция имеет обратную. Обратной к показательной функции является логарифмическая функция 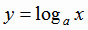 . Область
значений показательной функции - интервал
. Область
значений показательной функции - интервал 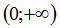 становится областью определения логарифмической функции, а область определения
показательной функции - множество всех действительных чисел
становится областью определения логарифмической функции, а область определения
показательной функции - множество всех действительных чисел 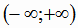 - областью значений логарифмической функции (рис. 1.6).
- областью значений логарифмической функции (рис. 1.6).
Рассмотрим подробно обратные тригонометрические функции.
Функция 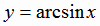 . На всей области определения - множестве всех действительных чисел
. На всей области определения - множестве всех действительных чисел 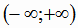 функция
функция 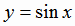 не имеет обратную, так как одному значению
не имеет обратную, так как одному значению 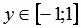 соответствует бесконечное множество значений
х (рис.1.7). Обратную функцию можно построить, если выделить из области определения функции
соответствует бесконечное множество значений
х (рис.1.7). Обратную функцию можно построить, если выделить из области определения функции 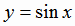 подмножество, на
котором эта функция монотонна. Выберем в качестве такого подмножества отрезок
подмножество, на
котором эта функция монотонна. Выберем в качестве такого подмножества отрезок 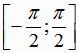 . На этом отрезке функция
. На этом отрезке функция
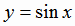 возрастает от -1 до 1, и, следовательно, имеет обратную с областью определения
возрастает от -1 до 1, и, следовательно, имеет обратную с областью определения 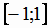 и областью
значений
и областью
значений 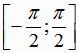 . Полученная обратная функция обозначается
. Полученная обратная функция обозначается 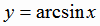 (рис. 1.13).
(рис. 1.13).
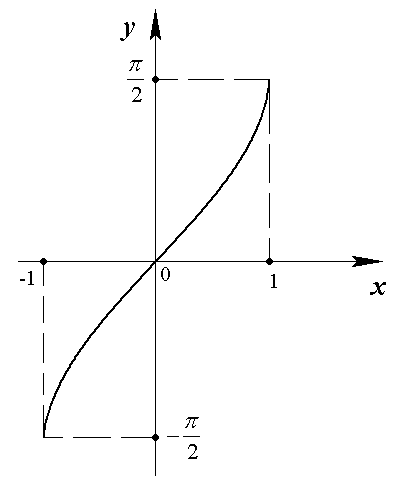
Рис. 1.13
Функция 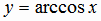 определяется как обратная по отношению к функции
определяется как обратная по отношению к функции 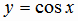 . Эта
функция, определенная на множестве действительных чисел
. Эта
функция, определенная на множестве действительных чисел 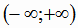 , на всей области определения обратную не имеет, так как одному
значению
, на всей области определения обратную не имеет, так как одному
значению 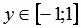 соответствует, как и для функции
соответствует, как и для функции 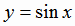 , бесконечное множество значений аргумента х
(рис.1.8). В качестве подмножества области определения, на котором функция
, бесконечное множество значений аргумента х
(рис.1.8). В качестве подмножества области определения, на котором функция 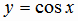 монотонна, выбран отрезок
монотонна, выбран отрезок 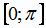 .
На этом отрезке функция убывает от 1 до -1, поэтому имеет обратную функцию, обозначаемую
.
На этом отрезке функция убывает от 1 до -1, поэтому имеет обратную функцию, обозначаемую 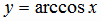 , с областью определения
, с областью определения 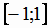 и областью значений
и областью значений 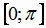 (рис. 1.14)
(рис. 1.14)
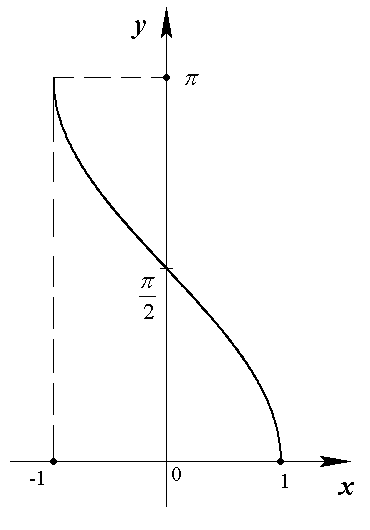
Рис. 1.14
Функция 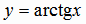 . Эта функция определяется как обратная по отношению к функции
. Эта функция определяется как обратная по отношению к функции 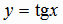 ,
если последнюю рассматривать на интервале
,
если последнюю рассматривать на интервале 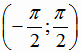 , на котором функция
, на котором функция 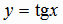 возрастает от
возрастает от
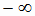 до
до 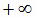 (рис. 1.9). Функция
(рис. 1.9). Функция 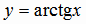 имеет область определения
имеет область определения 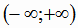 и область значений
и область значений 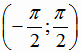 (рис. 1.15).
(рис. 1.15).
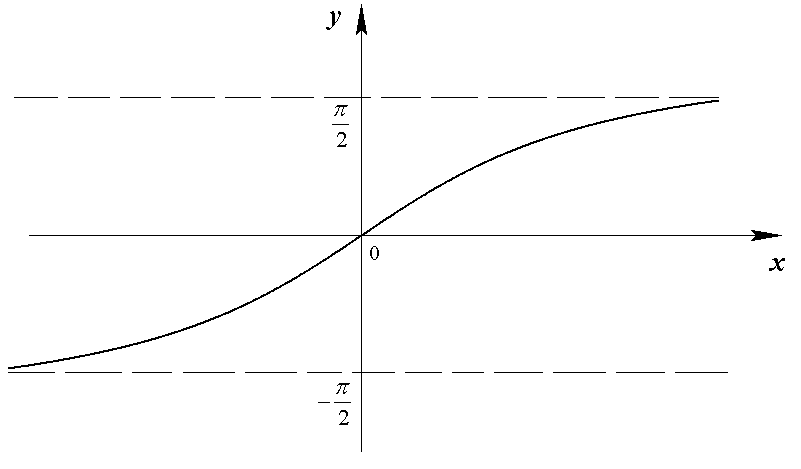
Рис. 1.15
Функция 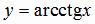 определяется как обратная по отношению к функции
определяется как обратная по отношению к функции 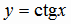 , если
последнюю рассматривать на интервале
, если
последнюю рассматривать на интервале 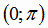 , на котором функция
, на котором функция 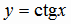 убывает от
убывает от 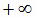 до
до 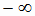 (рис.1.10). Функция
(рис.1.10). Функция 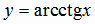 имеет область определения
имеет область определения 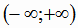 и область значений
и область значений
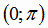 (рис. 1.16).
(рис. 1.16).
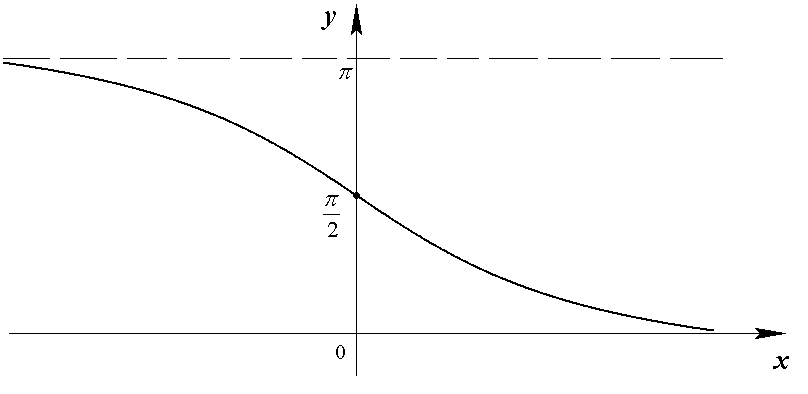
Рис. 1.16
Следующая страница
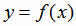 определена на множестве Х и имеет множество значений Y. Пусть эта
функция определяет взаимно однозначное соответствие между множествами Х и Y, т.е.
определена на множестве Х и имеет множество значений Y. Пусть эта
функция определяет взаимно однозначное соответствие между множествами Х и Y, т.е. 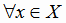 соответствует
единственное значение
соответствует
единственное значение 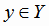 и, наоборот,
и, наоборот, 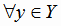 соответствует единственное значение
соответствует единственное значение 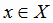 .
Тогда для каждого
.
Тогда для каждого 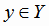 существует единственное значение х такое, что
существует единственное значение х такое, что 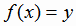 , и это соответствие
определяет функцию, называемую обратной по отношению к данной функции
, и это соответствие
определяет функцию, называемую обратной по отношению к данной функции 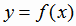 и обозначаемую
и обозначаемую 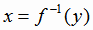 .
.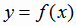 и её обратная функция
и её обратная функция 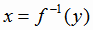 выражает одну и ту же связь между переменными
х и у. Но в первом случае мы рассматриваем х как независимую переменную, а у как функцию; во втором случае - наоборот:
у мы считаем независимой переменной, а х - функцией. График обратной функции
выражает одну и ту же связь между переменными
х и у. Но в первом случае мы рассматриваем х как независимую переменную, а у как функцию; во втором случае - наоборот:
у мы считаем независимой переменной, а х - функцией. График обратной функции 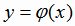 , т.е. независимую переменную обозначить х, значение функции - у и значения независимой
переменной откладывать на оси Ох, то график обратной функции будет симметричен графику функции
, т.е. независимую переменную обозначить х, значение функции - у и значения независимой
переменной откладывать на оси Ох, то график обратной функции будет симметричен графику функции 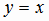 . При этом область значений функции
. При этом область значений функции 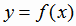 становится областью определения обратной функции
становится областью определения обратной функции 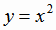 , если её рассматривать на
всей числовой оси, не имеет обратной функции, так как каждому значению
, если её рассматривать на
всей числовой оси, не имеет обратной функции, так как каждому значению 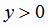 соответствует два значения
соответствует два значения 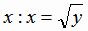 и
и 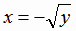 (рис.1.11). Если же функцию
(рис.1.11). Если же функцию 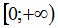 ,
то она имеет обратную функцию
,
то она имеет обратную функцию 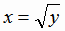 , так как на этом интервале каждому значению у соответствует единственное
значение х (рис. 1.11).
, так как на этом интервале каждому значению у соответствует единственное
значение х (рис. 1.11).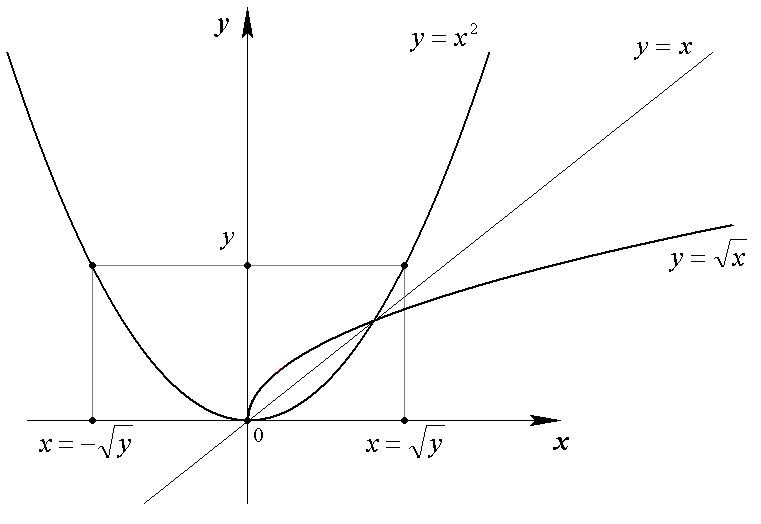
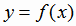 определена на множестве Х.
определена на множестве Х.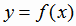 называется возрастающей на множестве Х, если для любых
называется возрастающей на множестве Х, если для любых 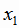 и
и 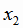 , принадлежащих Х, из условия
, принадлежащих Х, из условия 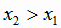 следует
следует 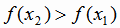 , т.е. большему значению
аргумента соответствует большее значение функции.
, т.е. большему значению
аргумента соответствует большее значение функции.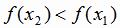 , т.е. большему значению
аргумента соответствует меньшее значение функции.
, т.е. большему значению
аргумента соответствует меньшее значение функции.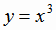 является возрастающей
на всей числовой оси; функция
является возрастающей
на всей числовой оси; функция 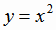 возрастает на промежутке
возрастает на промежутке 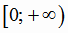 и убывает на промежутке
и убывает на промежутке
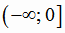 .
.
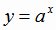 является строго монотонной на всей области определения. Если
является строго монотонной на всей области определения. Если 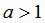 ,
то функция
,
то функция 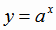 возрастающая, если
возрастающая, если 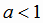 - убывающая (рис. 1.5). Поэтому на всей области определения
показательная функция имеет обратную. Обратной к показательной функции является логарифмическая функция
- убывающая (рис. 1.5). Поэтому на всей области определения
показательная функция имеет обратную. Обратной к показательной функции является логарифмическая функция 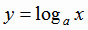 . Область
значений показательной функции - интервал
. Область
значений показательной функции - интервал 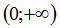 становится областью определения логарифмической функции, а область определения
показательной функции - множество всех действительных чисел
становится областью определения логарифмической функции, а область определения
показательной функции - множество всех действительных чисел 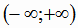 - областью значений логарифмической функции (рис. 1.6).
- областью значений логарифмической функции (рис. 1.6).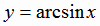 . На всей области определения - множестве всех действительных чисел
. На всей области определения - множестве всех действительных чисел 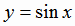 не имеет обратную, так как одному значению
не имеет обратную, так как одному значению 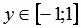 соответствует бесконечное множество значений
х (рис.1.7). Обратную функцию можно построить, если выделить из области определения функции
соответствует бесконечное множество значений
х (рис.1.7). Обратную функцию можно построить, если выделить из области определения функции 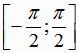 . На этом отрезке функция
. На этом отрезке функция
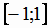 и областью
значений
и областью
значений 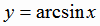 (рис. 1.13).
(рис. 1.13).
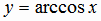 определяется как обратная по отношению к функции
определяется как обратная по отношению к функции 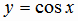 . Эта
функция, определенная на множестве действительных чисел
. Эта
функция, определенная на множестве действительных чисел 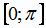 .
На этом отрезке функция убывает от 1 до -1, поэтому имеет обратную функцию, обозначаемую
.
На этом отрезке функция убывает от 1 до -1, поэтому имеет обратную функцию, обозначаемую 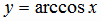 , с областью определения
, с областью определения 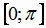 (рис. 1.14)
(рис. 1.14)
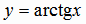 . Эта функция определяется как обратная по отношению к функции
. Эта функция определяется как обратная по отношению к функции 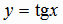 ,
если последнюю рассматривать на интервале
,
если последнюю рассматривать на интервале 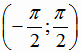 , на котором функция
, на котором функция 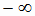 до
до 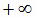 (рис. 1.9). Функция
(рис. 1.9). Функция 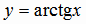 имеет область определения
имеет область определения 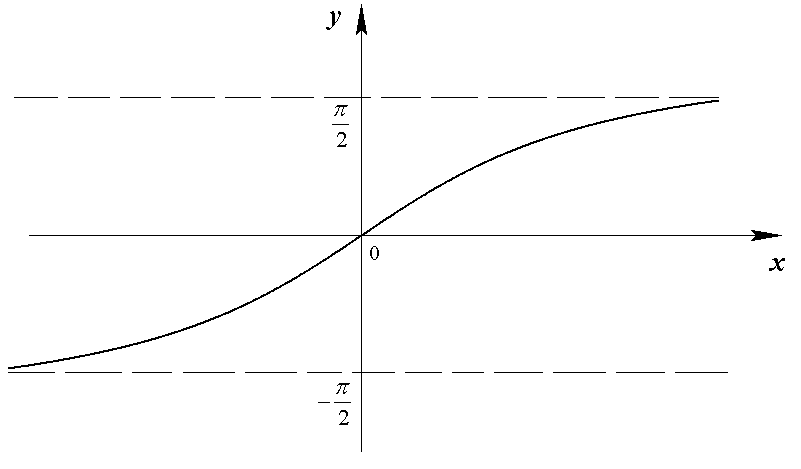
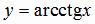 определяется как обратная по отношению к функции
определяется как обратная по отношению к функции 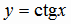 , если
последнюю рассматривать на интервале
, если
последнюю рассматривать на интервале 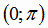 , на котором функция
, на котором функция 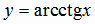 имеет область определения
имеет область определения