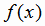 , определенная в симметричной относительно начала координат области Х, называется
четной, если для любого х из области определения выполняется условие:
, определенная в симметричной относительно начала координат области Х, называется
четной, если для любого х из области определения выполняется условие:Главная страница Предыдущая страница
1.2 Свойства функций: четность, нечетность, периодичность
При исследовании функций и построении их графиков важную роль играют некоторые их свойства. Здесь мы рассмотрим свойства четности, нечетности и периодичности.
Функция 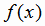 , определенная в симметричной относительно начала координат области Х, называется
четной, если для любого х из области определения выполняется условие:
, определенная в симметричной относительно начала координат области Х, называется
четной, если для любого х из области определения выполняется условие:
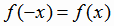 |
(1.1) |
График четной функции симметричен относительно оси ординат. Примерами четных функций являются степенная функция 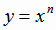 при четном n (рис. 1.2) функция
при четном n (рис. 1.2) функция 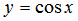 .
.
Функция 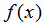 , определенная в симметричной относительно начала координат области Х, называется
нечетной, если для любого х из области определения выполняется условие:
, определенная в симметричной относительно начала координат области Х, называется
нечетной, если для любого х из области определения выполняется условие:
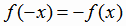 |
(1.2) |
График нечетной функции симметричен относительно начала координат. Примерами нечетных функций являются степенные функции
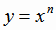 при нечетном n (рис. 1.1) в том числе и функция
при нечетном n (рис. 1.1) в том числе и функция 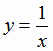 (рис. 1.3), тригонометрические
функции
(рис. 1.3), тригонометрические
функции 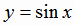 ,
, 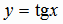 ,
, 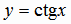 .
.
Функция 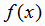 называется периодической, если существует такое положительное число Т (период
функции), что если для любого х из области определения выполняется условие:
называется периодической, если существует такое положительное число Т (период
функции), что если для любого х из области определения выполняется условие:
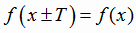 |
(1.3) |
При этом наименьшее из положительных чисел Т, обладающих вышеуказанным свойством, называется наименьшим периодом
функции 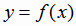 . Часто, говоря «период функции», имеют в виду наименьший период функции.
. Часто, говоря «период функции», имеют в виду наименьший период функции.
Тригонометрические функции 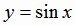 ,
, 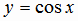 ,
, 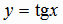 и
и 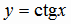 являются периодическими функциями. Для первых двух из них наименьший период равен
являются периодическими функциями. Для первых двух из них наименьший период равен 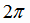 , две последние имеют наименьший период
, две последние имеют наименьший период
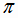 .
.
На практике часто встречаются тригонометрические функции вида 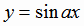 ,
, 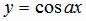 ,
, 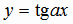 и
и  . Они также являются периодическими. Первые две из них имеют наименьший период
. Они также являются периодическими. Первые две из них имеют наименьший период 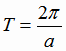 ,
две последние, соответственно,
,
две последние, соответственно, 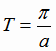 .
.