Главная страница

    1.1 Графики основных элементарных функций

    Рассмотрим основные элементарные функции. Так называются следующие функции:

    1. Постоянная (константа) , где С - действительное число. Графиком функции является прямая, параллельная оси абсцисс.

    2. Степенная функция , где n - действительное число, . Вид области определения степенной функции зависит от показателя n. Если n - натуральное число, имеем функции и т.д., для каждой из них область определения - вся числовая ось. Для нечетных n графики некоторых степенных функций приведены на рис. 1.1. Областью значений этих функций являются все действительные числа. Для четных n графики приведены на рис. 1.2. Для таких функций область значений - неотрицательные числа: .

Рис. 1.1

Рис. 1.2

     Из остальных степенных функций рассмотрим две. Первая из них 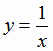определена на всей числовой оси, за исключением точки . Область значений - все действительные числа, за исключением . График этой функции приведен на рис. 1.3, он носит название гипербола. При стремлении х к +∞ и к -∞ значение функции стремится к нулю. График функции при этом стремится к прямой y = 0 (оси абсцисс). В этом случае говорят, что прямая y = 0 является горизонтальной асимптотой графика функции. При стремлении х к нулю с положительной стороны значение функции неограниченно возрастает, т.е. стремится к +∞. Когда же х стремится к нулю с отрицательной стороны, значение функции стремится к -∞. График функции при этом стремится к прямой х = 0 (оси ординат). В этом случае говорят, что прямая х = 0 является вертикальной асимптотой графика функции. Таким образом, график функции 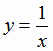имеет горизонтальную асимптоту y = 0 и вертикальную асимптоту х = 0.

Рис. 1.3

    Вторая функция определена для и имеет график, изображенный на рис. 1.4, область значений - неотрицательные числа .

Рис. 1.4

    3. Показательная функция (). Эта функция определена для всех действительных х. На рис. 1.5 приведены графики показательных функций для и для . Область значений показательной функции - положительные числа

Рис. 1.5

     4. Логарифмическая функция . Область определения логарифмической функции - положительные числа , область значений - все действительные числа. Графики (для и для ) изображены на рис. 1.6.

Рис. 1.6

    5. Тригонометрические функции , , и . Графики тригонометрических функций и изображены на рис. 1.7 и рис. 1.8. Каждая из них определена на всей числовой оси. Областью значений является отрезок .

Рис. 1.7

Рис. 1.8

    Функция определена на всей числовой оси, за исключением точек вида , а функция - на всей числовой оси, кроме точек (n - любое целое число). Графики этих функций изображены на рис. 1.9 (в пределах от до ) и рис. 1.10 (в пределах от до ).

Рис. 1.9

Рис. 1.10

    6. Обратные тригонометрические функции , , ,

Следующая страница