Главная страница     Предыдущая страница

    1.2 Расчёт вероятностей с помощью правил сложения и умножения

    Совмещением А· В двух событий А и В называют общую часть множеств исходов, составляющих события А и В (в результате испытания происходят оба события: А и В). Условной вероятностью Р(В/А) называется вероятность события В при условии осуществления события А. Вероятность совмещения двух событий находится по формуле

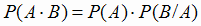(1.2)

    Вероятность совмещения двух событий равна произведению вероятности одного из них на условную вероятность другого.

    Пример 1.2. Студент знает правильный ответ на 20 экзаменационных вопросов из 30. Какова вероятность того, что он:

    а) знает ответ на два заданных ему вопроса;

    б) не знает ответа на оба заданных ему вопроса?

    Решение: Пусть событие А = {студент знает ответ на первый вопрос}, В = {студент знает ответ на второй вопрос}. Р(А) = 20/30. Р(В/А) = 19/29 (из 29 оставшихся вопросов студент знает ответ на 19, так как на один из известных ему вопросов он уже ответил). Тогда Р(А · В) = Р (студент знает два вопроса) = Р(А) · Р(В/А) = .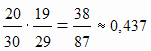

    Пусть событие С = {студент не знает ответ на первый вопрос}, D = {студент не знает ответ на второй вопрос}. Р(С) = 10/30. Р(С/D) = 9/29 (из 29 оставшихся вопросов студент не знает ответ на 9, так как на один из вопросов он уже не ответил). Тогда Р(А · В) = Р (студент не знает два вопроса) = Р(А) · Р(В/А) = .

    Формула (1.2) обобщается для трех событий А, В, С:

    Пример 1.3. Из колоды в 52 карты случайным образом берут 3 карты. Найти вероятность того, что все три карты - тузы (событие D).

    Решение: D = А · В · С, где А = { первая карта - туз}, В = { вторая карта - туз}, С = {третья карта - туз}. В силу равной возможности исходов, обеспеченной перемешиванием карт, здесь можно воспользоваться классической формулой (1.1), как для расчёта безусловных, так и для расчёта условных вероятностей. Р(А) = 4/52 (в колоде из 52 карт 4 туза), Р(В/А) = 3/51 (осталась 51 карта, среди них - 3 туза), Р(С/(А · В)) =2/50 (осталось 50 карт, среди них - 2 туза). Тогда по формуле (1.9)

Р(D) = Р (три туза) = 4/52 · 3/51 · 2/50 = 0,00018

    Суммой случайных событий А и В называется событие С, соответствующее объединению множеств А и В (С = А + В). В этом случае можно сказать, что произойдет хотя бы одно из событий А и В (или только событие А, или только событие В, или оба вместе).

    События А и В называются несовместными, если они не могут произойти одновременно при одном и том же испытании, т. е. если пересечение множеств А и В пусто. Для несовместных событий А и В

    Суммой случайных событий А₁, А₂, ..., А_n называется событие. соответствующее объединению множеств А₁, А₂, ..., А_n. Здесь также можно сказать, что суммой событий является событие при котором произойдет хотя бы одно из указанных событий.

    Формула (1.4) обобщается для попарно несовместных событий А₁, А₂, ..., А_n:

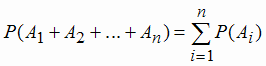(1.5)

    Пример 1.4. Мишень состоит из центрального круга - “яблочка” и двух концентрических колец. Вероятности попадания в “яблочко” и кольцо соответственно равны 0,2; 0,25; 0,35. Найти вероятность попадания в мишень (событие D).

    Решение: Событие А₁ = {попадание в “яблочко”}, А_2,3 = {попадание в одно из колец} попарно несовместны и D = A₁ + A₂ + A₃. По правилу сложения вероятностей

Р(А₁ + А₂ + А₃) = Р(А₁) + Р(А₂) + Р(А₃) = 0,2 + 0,25 + 0,35 = 0,8

    События А₁, А₂, ..., А_N образуют полную группу, если они попарно несовместны и одно из них обязательно должно произойти при рассматриваемом испытании, т. е. их сумма есть достоверное событие:

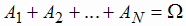
    При этом

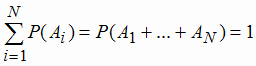(1.6)

    Два события А и 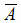называются противоположными, если они образуют полную группу: 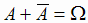(при этом появление одного из них равносильно непоявлению другого). Так как , то по вероятности одного из противоположных событий можно находить вероятность другого:

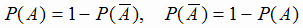(1.7)

Следующая страница