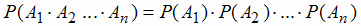 ,
,Главная страница Предыдущая страница
1.3 Независимость случайных событий
Для двух независимых событий А и В правило умножения вероятностей имеет вид:
| Р(А · В) = Р(А) · Р(В) | (1.8) |
Сравнивая с формулой (1.2), видим, что их условные вероятности равны безусловным, т. е.
Р(В/А) = Р(В); Р(А/В) = Р(А).
Формула (1.8) может быть обобщена на независимые в совокупности события А1, ..., Аn:
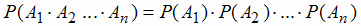 , , |
(1.9) |
вероятность их совмещения равна произведению вероятностей.
Рассмотрим примеры, где применяются правила сложения и умножения независимых событий. Отметим одно полезное при решении
задач свойство: если события А и В независимы, то будут независимыми следующие пары событий: 1) А и 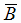 ;
2)
;
2) 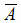 и В; 3)
и В; 3) 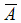 и
и 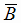 и тогда
и тогда

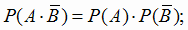 |
(1.10) |

Пример 1.5. Два стрелка стреляют по мишени независимо друг от друга по одному разу. Вероятности попадания равны: для первого стрелка Р(А1) = 0,7, для второго стрелка Р(А2) = 0,8. Найти вероятности событий:
а) в мишени ровно одна пробоина (событие С);
б) мишень поражена (событие D)
Решение: а) Событие С = (попадет или только первый стрелок {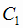 } или только второй
стрелок {
} или только второй
стрелок {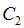 }) = С1 + С2, где события С1 и С2
несовместны и по правилу сложения (1.4) Р(С) = Р(С1) + Р(С2).
}) = С1 + С2, где события С1 и С2
несовместны и по правилу сложения (1.4) Р(С) = Р(С1) + Р(С2).
Событие 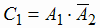 (первый стрелок попал, второй не попал), в силу независимости событий А1
и А2 (по условию задачи), будут независимыми события А1 и
(первый стрелок попал, второй не попал), в силу независимости событий А1
и А2 (по условию задачи), будут независимыми события А1 и 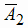 и
и
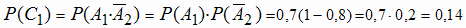 .
.
Аналогично, 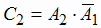 (второй стрелок попал, первый - не попал) и Р(С2) =
(второй стрелок попал, первый - не попал) и Р(С2) = 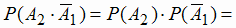 0,8(1
- 0,7) = 0,8 · 0,3 = 0,24. Тогда
0,8(1
- 0,7) = 0,8 · 0,3 = 0,24. Тогда 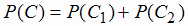 = 0,14 + 0,24 = 0,38.
= 0,14 + 0,24 = 0,38.
б) Событие D = {мишень поражена} = {попадет хотя бы один стрелок} = A1 + A2
(попадет или первый стрелок, или второй стрелок, или оба вместе), где события А1 и А2 совместны и, обратите
внимание, правило (1.4) применять нельзя. Перейдем к противоположному событию 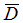 .
.
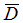 = {мишень не поражена} =
= {мишень не поражена} = 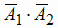 = (первый стрелок не попал и второй стрелок
не попал), где
= (первый стрелок не попал и второй стрелок
не попал), где 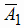 и
и 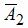 - независимые события. Тогда
- независимые события. Тогда  = (1 - 0,7)(1
- 0,8) = 0,3 · 0,2 = 0,06.
= (1 - 0,7)(1
- 0,8) = 0,3 · 0,2 = 0,06.
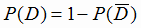 = 1 - 0,06 = 0,94
= 1 - 0,06 = 0,94
Для вычисления вероятности появления хотя бы одного из событий А1, А2, ..., Аn
можно найти сначала вероятность противоположного события, которое заключается в том, что не произойдет ни одно из указанных событий. Это событие
соответствует совмещению событий, противоположных рассматриваемым: 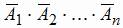 .
.
Окончательная формула будет:
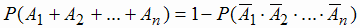 |
(1.11) |
Независимость трех событий А, В и С в совокупности означает выполнимость четырех условий:
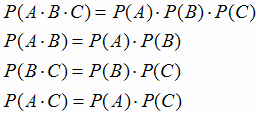 |
(1.12) |
Пример 1.6. Три элемента в системе работают независимо друг от друга. Вероятности безотказной работы равны: для первого элемента Р(А1) = 0,6; для второго элемента Р(А2) = 0,7; для третьего элемента Р(А3) = 0,8. Найти вероятности следующих событий - в системе будут работать безотказно:
а) только один элемент (событие В);
б) только два элемента (событие С);
в) все три элемента (событие D);
г) хотя бы один элемент (событие F).
Решение: а) Событие 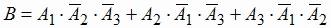 (один элемент работает, при этом два других не работают). В силу
независимости событий А1, А2, А3 по правилам сложения и умножения вероятностей
(один элемент работает, при этом два других не работают). В силу
независимости событий А1, А2, А3 по правилам сложения и умножения вероятностей
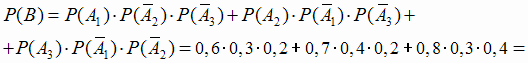
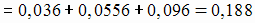
б) Событие 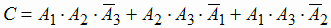 (два элемента работают, при этом третий не работает)
(два элемента работают, при этом третий не работает)
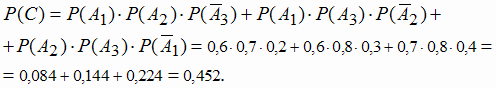
в)  и по правилу (1.9) для независимых событий:
и по правилу (1.9) для независимых событий:
 0,6 · 0,7 · 0,8 = 0,336.
0,6 · 0,7 · 0,8 = 0,336.
г) 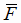 = {все три элемента не работают} =
= {все три элемента не работают} =  .
.
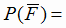 0,4 · 0,3 · 0,2 = 0,024;
0,4 · 0,3 · 0,2 = 0,024; 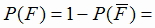 1 - 0,024 = 0,976.
1 - 0,024 = 0,976.