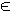Ω . Число исходов, входящих в пространство Ω может быть конечным или бесконечным.1 Теоретическое введение
1.1 Непосредственный расчёт вероятностей
Событием называется эксперимент с двумя возможными исходами («да» или «нет»). Случайным называется такое событие, результат которого нельзя предсказать до проведения эксперимента.
Рассмотрим множество Ω всех возможных, взаимно исключающих друг друга, исходов некоторого испытания (эксперимента).
Это множество будем называть пространством элементарных исходов, а сами эти исходы будем рассматривать, как точки ω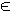
Ω . Число исходов, входящих в пространство Ω может быть конечным или бесконечным.
Случайное событие А есть некоторое множество точек пространства Ω т.е. некоторое подмножество множества
Ω . Если при испытании осуществился исход ω 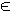А, то говорят, что произошло событие А. В частности,
если А = Ω , то событие называется достоверным, если А = ø , то событие называется невозможным.
С каждым событием А связывается число р(А) - вероятность события А, отражающее степень
объективной возможности наступления этого события. Вероятность достоверного события равна единице, вероятность невозможного события равна нулю,
для всех остальных событий А: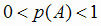 
.
Наиболее просто вероятность находится в классической модели -эксперименте удовлетворяющем двум условиям:
1) множество элементарных исходов конечно Ω = {ω 1, ω 2, ..., ω N};
2) все исходы испытания равновозможны.
Равновозможность исходов устанавливается либо из соображений симметрии, как при подбрасывании монеты (мы считаем, что герб и решка равновозможны), при бросании игрального кубика (выпадения любого числа очков от 1 до 6 равновозможны), либо из условия тщательного предварительного “перемешивания” исходов, как при розыгрыше лотереи, игре в карты, “Домино” и т. п.
В этом случае полагают, что вероятность любого исхода события А одинаков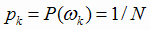а 
и вероятность
любого события А равна
 , |
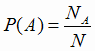(1.1) |
где NA - число исходов, входящих в множество А, или, как обычно говорят, число исходов, благоприятствующих событию А; N - общее число возможных исходов.
Пример 1.1. 13 человек рассаживается за круглым столом случайным образом. Найти вероятность того, что Иванов и Петров окажутся рядом.
Решение: Пусть Иванов сел на произвольное место за столом. Для Петрова осталось 13 - 1 = 12 мест, N = 12, около Иванова есть только два соседних места, слева и справа, т. е. NA = 2, поэтому
.
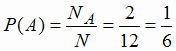