Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Метод соответственной полосы

    Несколько более сложным, но более обоснованным с позиций теории подобия является метод соответственной полосы. А.Ф.Головин (1933 г.) предложил ввести в соответствие профилю любой формы равновеликий ему по площади прямоугольник, у которого отношение сторон будет такое же, как и отношение сходственных осей профиля. Например, полоса, соответственная профилю квадратной заготовки, задаваемой в калибр, будет иметь такую же площадь F₀ и отношение сторон b_0с/h_0с=b₀/h₀=1; полоса, соответственная прокатанному ромбическому профилю, будет иметь площадь F₁ при отношении сторон b_1с/h_1с=b₁/h₁. Высоту и ширину соответственной полосы можно рассчитать по формулам:

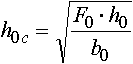
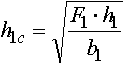
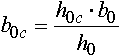
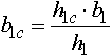
    Метод соответственной полосы получил дальнейшее развитие в работах В.С. Смирнова, К.Н. Богоявленского и Н.Н. Павлова.

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.