 |
Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru |
| На главную | Контакты | Выполнить расчёт (запустить приложение) |
|
|||
|
Анализ метода соответственной полосы
В.С. Смирнов и его сотрудники развили этот метод и показали, что расхождение опытных и расчётных значений Fк не превышает 10 %.
Подобными условиями деформации называются такие, при которых удовлетворены условия геометрического, физического и механического подобия. Геометрически подобными называются такие тела, отношение характерных площадей сечения которых равно квадрату отношения их линейных размеров, а отношение объёмов равно кубу отношения их линейных размеров:
F'/F"=1, V'/V"=1
и, следовательно: F'=F", V'=V", т.е. размеры модели и натуры совпадают.
Понятно, что ввиду различия геометрической формы соответственных полос можно говорить лишь об их приближенном геометрическом подобии.
Пусть мы имеем некоторый фасонный профиль и его требуется преобразовать к профилю прямоугольной формы.
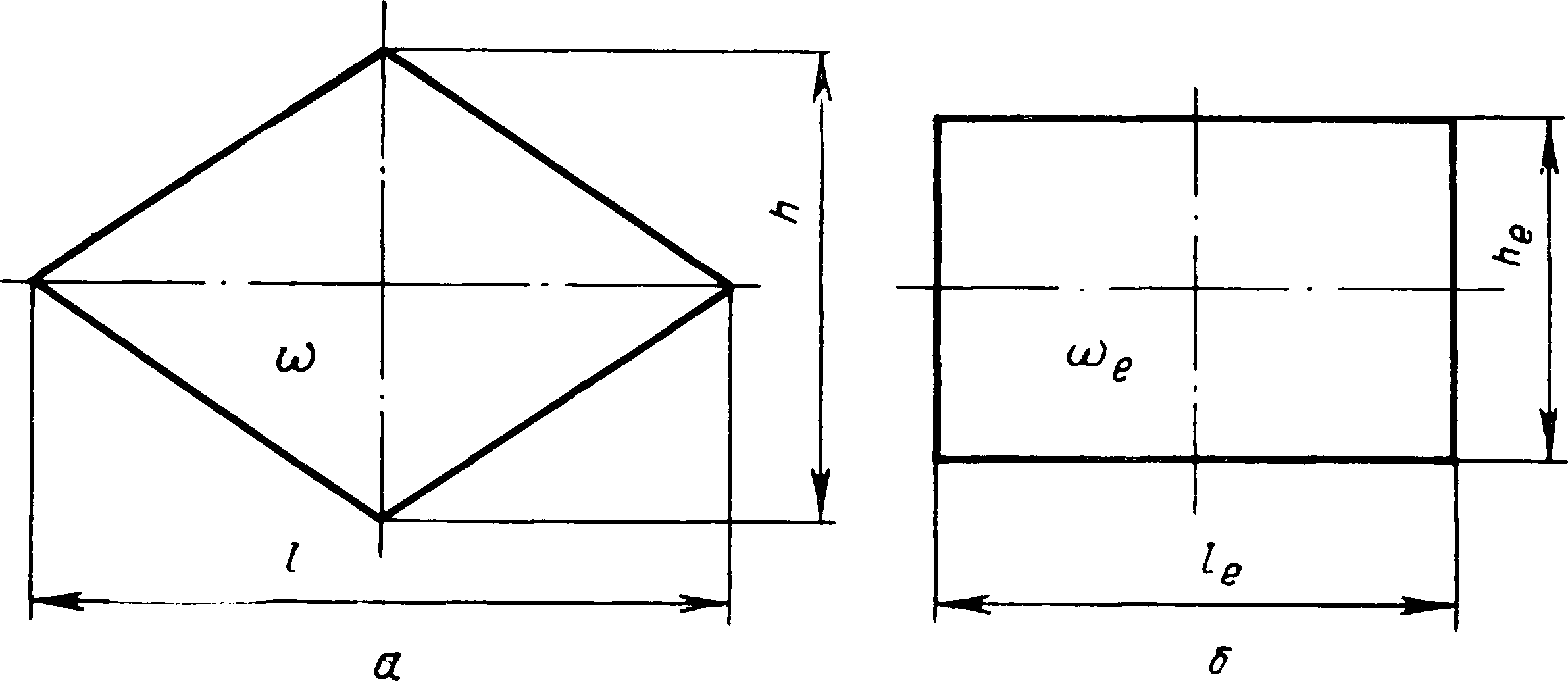
Рис. Фасонный и соответствующие ему прямоугольный профили
Введем следующие обозначения:
h, b, A=b/h, F - высота, ширина, отношение ширины
к высоте и площадь фасонного профиля;
hc, bc, Ac=bc/hc,
Fc - те же величины для соответственного прямоугольного профиля.
Размеры соответственных профилей связаны между собой формулами, вытекающими из их определения:
bс=A·hс; F=hс·bс.
Откуда
| hс=√(F/A); bс=A·hс | (1) |
Условия постоянства объёма для соответственной прямоугольной полосы можно написать в следующем виде:
[(h1·C)/(h0·C)]·[(b1·C)/(b0·C)]·[(l1·C)/(l0·C)]=1
или
ηc·βc·λc=1.
Для полос фасонного сечения условие постоянства объёма по форме может точно совпадать с записанными выше или отличаться от него численными множителями, зависящими от формы поперечных сечений полосы до и после прокатки. Например, при прокатке ромбического сечения в ромбическое этот множитель равен 1, а при прокатке квадрата в эллипс √π/2.
Эти коэффициенты учитывают различие в значениях высоты и ширины профиля по его сечению, и поэтому их уместно называть коэффициентами преобразования сечения. Тогда условие постоянства объёма можно записать в таком виде:
| γ2·(h1/h0)·(b1/b0)·(l1/l0)=1 | (4) |
или
| γη·(h1/h0)·γβ·(b1/b0)·(l1/l0)=1 | (5) |
причем
| γ2=γη·γβ | (6) |
Равенство (5) можно переписать так:
| η·β·λ=1, | (7) |
где коэффициенты деформации полосы равны:
η=γη·(h1/h0);
| β=γβ·(b1/b0) | (8) |
λ=l1/l0.
В равенствах (4)-(8) γ, γη, γβ - коэффициенты преобразования сечения по площади, по высоте и по ширине.
Для полос фасонного сечения напишем следующее соотношение:
M=A1/A0=(b1/h1)/(b0/h0)= (b1/b0)·(h0/h1)
Имеем
M=(γη/γβ)·(β/η)
Откуда:
β=M·(γβ/γη)·η
С учётом этого соотношения условие постоянства объёма приобретает вид:
M·(γβ/γη)·η2·λ=1,
откуда:
η=1/√(M·λ·γβ/γ) (9,а)
Для соотвественных полос запишем ряд соотношений:
Mc=(A1·C)/(A0·C)=[(b1·C)/(h1·C)]/[(b0·C)/(h0·C)]=[(l1·C)/(b0·C)]·[(h0·C/(h1·C)] (9,б)
Mc=βc/ηc; βc=Mc·ηc;
Mc·ηc2·λ=1; ηc=1/√(Mc·λ).
Имея в виду, что отношение осей у соответственных полос одинаково, убеждаемся в том, что M=Mс.
Далее, вытяжки у соответственных полос одинаковы по определению. Поэтому для того, чтобы коэффициенты деформации соответственных полос по высоте были одинаковы, необходимо, чтобы выполнялось условие
gb=gh=g, (9,с)
что следует из сравнения соотношений (9,а) и (9,б). Тогда из условия постоянства объёмов немедленно будет следовать и равенство приведенных коэффициентов деформации соответственных полос по ширине. Опыты, проведенные А.К. Григорьевым и Н.Х. Давильбековым, доказали, что соотношение (5) для простых профилей соблюдается.
Итак, поскольку коэффициент преобразования сечения у соответственных полос по ширине и высоте одинаков, то коэффициенты их деформации по высоте, ширине и длине также одинаковы, т.е.
(h0·C)/(h1/C)=1/ηc=1/η=1/γ·(h0/h1); (9,д)
(b1·C)/(b0·C)=βc=β=γ·b1/b0;
λc=λ.
Эти исходные соотношения дают возможность далее доказать, что для соответственных профилей одинаковы объёмы, заключенные в пределах очага деформации; объёмы, смещенные по длине, высоте и ширине очага деформации; секундные объёмы, средняя длина, ширина и площадь горизонтальной проекции очага деформации; опережение и отставание; отношение площади контактной поверхности к объёму очага деформации. Наконец, отношения полных поверхностей к объёму очага деформации равны в первом приближении. Итак, геометрическое подобие для соответственных полос соблюдается с хорошей степенью приближения.
Если тела геометрически подобны, то условия их механического подобия сводятся к тому, чтобы в случае аналогичного по характеру статического нагружения внешними силами Р и давлениями p, значения этих величин у натуры и у модели были равны между собой P/F=idem или p=idem.
Характер статического нагружения у фасонной и прямоугольной соответственных полос различен, поэтому точное соблюдение условий механического подобия в данном случае невозможно.
Следует иметь в виду, что проведенные выше рассуждения относились к соответственной прямоугольной полосе, которая представляет собой некоторый расчётный эквивалент фасонного профиля. Возникает вопрос, в какой мере этот расчётный эквивалент соответствует действительным условиям прокатки прямоугольной полосы на гладкой бочке. Опыты Н.Н. Павлова показали, что поверхности контакта прямоугольных полос отличались по величине от поверхностей контакта фасонных полос с валками в большую сторону.
Это объясняется следующими причинами.
Равенство коэффициентов деформации при прокатке фасонных полос и соответственных им расчётных, как было показано выше, вытекает из условия постоянства объёма и из того факта, что объёмы, заключенные в пределах очага деформации, и объёмы, смещаемые по высоте, ширине и длине, у таких полос одинаковы. Характер действующих в калибрах и на гладкой бочке сил в данном случае не учитывается, поскольку речь идет о простом пересчёте геометрических размеров полос до и после прокатки по формулам (1) преобразования сечений.
При практическом осуществлении прокатки фасонной полосы в калибрах и прямоугольной полосы, исходные размеры которой равны соответственным на гладкой бочке, возникает система сил, зависящая от размеров и формы калибра и полосы и от степени заполнения калибра. Иными словами, несоответствие коэффициентов деформации в данном случае обусловлено различием в статической системе сил, приложенных со стороны калибра к полосе фасонного профиля и со стороны бочки валков к полосе прямоугольного профиля.
Это различие можно учесть при помощи эмпирических поправочных коэффициентов уширения. В результате коэффициенты деформации фасонного профиля в калибре и прямоугольного на гладкой бочке будут одинаковы, т.е. они будут соответственными.
Однако поправка на уширение важна для расчёта деформации полосы, а не расчёта давлений на валки. Если размеры полосы до и после прокатки известны, то расчёт давлений будет достаточно точным и без введения поправки на уширение. Это следует из многочисленных опытов, которые показывают, что характер статического нагружения оказывает слабое влияние на величину среднего давления при прокатке фасонных полос: p=pc. Объясняется это тем, что при прокатке фасонных полос, в элементах сечения полосы, имеющих обжатие, отличное от среднего, возбуждаются дополнительно осевые сжимающие напряжения в зонах повышенного обжатия и растягивающие напряжения в зонах пониженного обжатия (±σ'ρ) вследствие одинаковой для всего сечения вытяжки. Дополнительные напряжения, в соответствии с уравнением пластичности, увеличивают или уменьшают контактные напряжения в этом сечении:
σψ=K+(σρ+σ'ρ).
Осевые напряжения σ'ρ взаимно уравновешиваются, т.е. их алгебраическая сумма по всему сечению полосы равна нулю. Поэтому на среднее давление прокатки эти дополнительные напряжения влияния не оказывают.
Итак, можно принять, что средние давления при прокатке соответственных полос одинаковы. Вместе с тем выше было показано, что площади контактных поверхностей у соответственных полос одинаковы. Следовательно, суммарное давление на валки соответственных полос также одинаково:
P=p·F=pc·Fc=Pc.
Отсюда следует, что и работа прокатки, затрачиваемая на деформацию соответственных полос, одинакова: A=Ac.
Это следует из того, что коэффициенты деформации, объёмы, заключенные в пределах очага деформации, и давления при прокатке соответственных полос одинаковы:
A=p·W·ln λ=pc·Wc·ln λc=Ac.
Итак, различие в характере статического нагружения не вносит существенного различия между величинами средних и суммарных давлений, а также работ прокатки соответственных полос.
Все изложенное дает нам право производить расчёты давления на валки, работы, момента и мощности прокатки простых профилей, используя достаточно обоснованный с позиций теории подобия метод соответственной полосы.