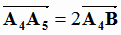 ,где B - точка пересечения вышеуказанной прямой и плоскости. Напишем параметрическое уравнение
прямой A4A5 по формуле:
,где B - точка пересечения вышеуказанной прямой и плоскости. Напишем параметрическое уравнение
прямой A4A5 по формуле:Главная страница Предыдущая страница
Задача 6. Точка A5, симметричная точке A4 относительно плоскости A1A2A3,
определяется следующим образом (рис. 1.10): прямая A4A5 перпендикулярна плоскости A1A2A3
и 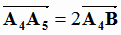 ,где B - точка пересечения вышеуказанной прямой и плоскости. Напишем параметрическое уравнение
прямой A4A5 по формуле:
,где B - точка пересечения вышеуказанной прямой и плоскости. Напишем параметрическое уравнение
прямой A4A5 по формуле:
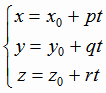
где 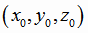 произвольная точка прямой,
произвольная точка прямой,
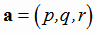 - направляющий вектор прямой.
- направляющий вектор прямой.
Воспользуемся тем фактом, что нормальный вектор плоскости 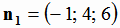 (см. задачу 1), является направляющим
вектором искомой прямой:
(см. задачу 1), является направляющим
вектором искомой прямой:
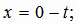 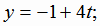 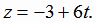 |
(1.25) |
Найдем координаты точки 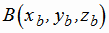 . Для этого подставим (x, y, z) из формулы (1.25)
в уравнение плоскости (1.24):
. Для этого подставим (x, y, z) из формулы (1.25)
в уравнение плоскости (1.24):
-(-t) +4(-1 + 4t) +6(-3 +6t) -31=0; 53t = 53; t = 1.
Следовательно,
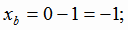
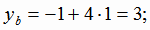
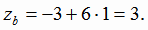
Тогда 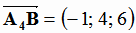 и
и 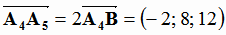 . Зная координаты вектора
. Зная координаты вектора 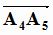 и координаты
его начала A4, легко найти координаты конца
и координаты
его начала A4, легко найти координаты конца 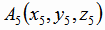 :
:
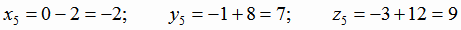 .
.
Для контроля полученного результата вновь вычислим высоту пирамиды h как половину отрезка А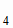 А
А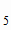 (рис. 1.10):
(рис. 1.10):
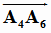 = ( -2; 8; 12); h =
= ( -2; 8; 12); h = 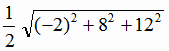 =
= 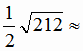 7,28.
7,28.
Совпадение с предыдущими расчётами говорит о правильности нахождения координат точки А5.
Ответ: (-2; 7; 9).
Задача 7. Точка A6, симметричная точке A4 относительно прямой A2A3,
определяется следующим образом: прямая A4A6перпендикулярна прямой A2A3 и пересекает
её и 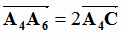 , где C - точка пересечения этих прямых (рис. 1.11). Заметим, что прямая A4A6
с нужными нам свойствами принадлежит плоскости π , проходящей через точку A4 перпендикулярно прямой A2A3,
так как плоскость π содержит все прямые, проходящие через точку A4 перпендикулярно A2A3.
Нормальным вектором к плоскости π можно считать вектор
, где C - точка пересечения этих прямых (рис. 1.11). Заметим, что прямая A4A6
с нужными нам свойствами принадлежит плоскости π , проходящей через точку A4 перпендикулярно прямой A2A3,
так как плоскость π содержит все прямые, проходящие через точку A4 перпендикулярно A2A3.
Нормальным вектором к плоскости π можно считать вектор 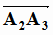 :
:
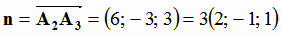 .
.
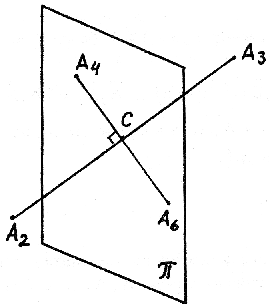
Рис. 1.11.
Напишем уравнение плоскости π , используя формулу (1.7):
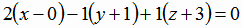 |
(1.26) |
Напишем параметрические уравнения прямой A2A3, зная её направляющий вектор (2;-1; 1)
| x = 1 + 2t; y = 5 - t; z = 2 + t | (1.27) |
Найдем координаты точки 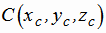 , подставляя выражения (1.27) в формулу (1.26):
, подставляя выражения (1.27) в формулу (1.26):
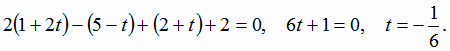
Следовательно,
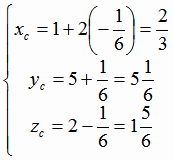
Тогда 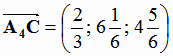 и
и 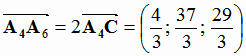 .
.
Окончательно находим координаты точки 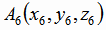 :
:
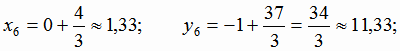
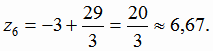
Ответ: (1,33; 11,33; 6,67).
Задача 8. Вычислим расстояние L между точкой А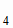 и прямой А
и прямой А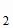 А
А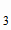 двумя способами:
двумя способами:
1. L 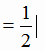
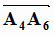
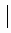 =
=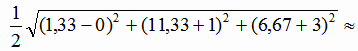 7,86.
7,86.
2. Расстояние L от точки 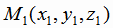 до прямой, заданной уравнением
до прямой, заданной уравнением
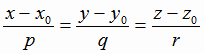 ,
,
где 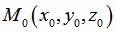 - произвольная точка прямой,
- произвольная точка прямой, 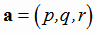 - направляющий вектор прямой, вычисляется по формуле:
- направляющий вектор прямой, вычисляется по формуле:
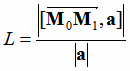
В этой формуле положим М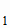 = А
= А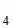 , М
, М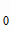 = А
= А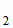 ,
a =
,
a = 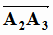 , тогда
, тогда
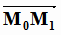 = (-1; -6; -5); a = ( 6; -3; 3);
= (-1; -6; -5); a = ( 6; -3; 3);
[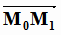 , a ] =
, a ] = 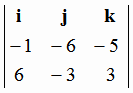 =
= 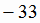 i
-27j +39k;
i
-27j +39k;
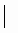 [
[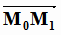 , a ]
, a ]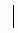 =
= 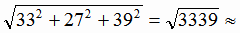 57,78;
57,78;
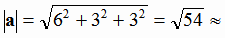 7,35; L =
7,35; L = 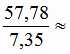 7,86.
7,86.
Совпадение результатов расчёта двумя способами свидетельствует о правильности нахождения координат точки А .
.
Ответ: 7,86.
Задача 9: Расстояние между скрещивающимися прямыми вычисляется по формуле:
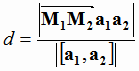 ,
,
где 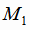 и
и 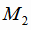 произвольные точки первой и второй прямой,
произвольные точки первой и второй прямой, 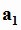 и
и 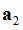 - их направляющие вектора. Для вычисления расстояния между ребрами A1A3 и A2A4 воспользуемся
формулой (1.18), в которой положим
- их направляющие вектора. Для вычисления расстояния между ребрами A1A3 и A2A4 воспользуемся
формулой (1.18), в которой положим
M1=A1; M2=A2, 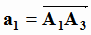 ;
; 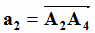 ;
;
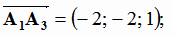
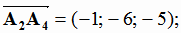
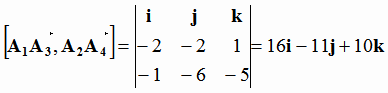 ;
;
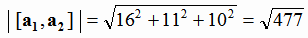 ;
; 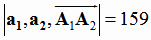 .
.
(см. задачу 4). Окончательно получаем:
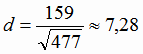
Ответ: 7,28.
Задача 10. Центр описанного около пирамиды шара является точкой, равноудаленной от его вершин A1,
A2, A3, A4. Обозначим координаты этой точки 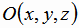 . Имеем
. Имеем
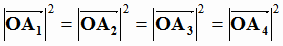
или
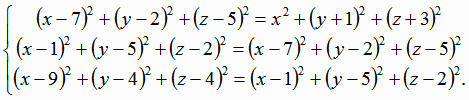
Раскроем скобки, приведем подобные члены и получим систему линейных уравнений:
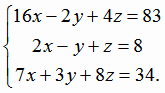
Решим эту систему по формулам Крамера:
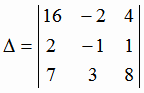 = -106;
= -106; 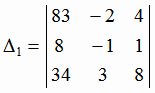 = -621;
= -621;
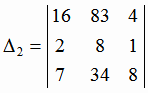 = -219;
= -219; 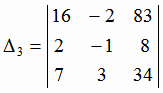 = 175.
= 175.
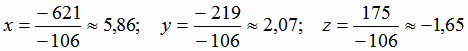
Радиус описанной сферы вычислим как расстояние от его центра до вершины, например, вершины 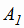 :
:
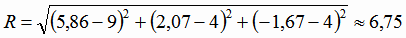
Ответ: (5,86; 2,07; -1,65), R=6,75.