 к плоскости A1A2A3,
найдем сначала векторное произведение векторов
к плоскости A1A2A3,
найдем сначала векторное произведение векторов 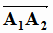 и
и 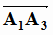 .
.Главная страница Предыдущая страница
5 Пример выполнения типового расчёта
Условие типового расчёта.
По условию имеем следующие координаты вершин пирамиды:
A1 (9; 4; 4), A2 (1; 5; 2), A3 (7; 2; 5), A4 (0; -1; -3).
Задача 1. Чтобы найти нормаль n к плоскости A1A2A3,
найдем сначала векторное произведение векторов
к плоскости A1A2A3,
найдем сначала векторное произведение векторов 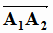 и
и 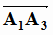 .
.
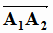 = (-8; 1; -2) ;
= (-8; 1; -2) ; 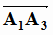 = (-2; -2; 1);
= (-2; -2; 1);
[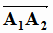 , ,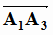 ] = ] = 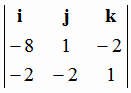 = -3i
+ 12j + 18k = -3i
+ 12j + 18k |
(1.22) |
За нормаль n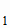 можно взять любой вектор, коллинеарный вектору (1.22). Для упрощения дальнейших
расчётов поделим координаты вектора (1.22) на общий множитель 3, получим коллинеарный вектор, его и примем за вектор n
можно взять любой вектор, коллинеарный вектору (1.22). Для упрощения дальнейших
расчётов поделим координаты вектора (1.22) на общий множитель 3, получим коллинеарный вектор, его и примем за вектор n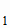 .
.
n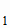 = ( -1; 4; 6) = ( -1; 4; 6) |
(1.23) |
Аналогично находим нормаль n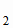 к плоскости
к плоскости 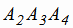 :
:
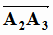 = ( 6; -3; 3) ;
= ( 6; -3; 3) ; 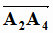 = ( -1; -6; -5);
= ( -1; -6; -5);
[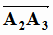 ,
,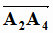 ] =
] = 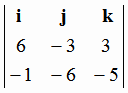 = 33i
+ 27j - 39k;
= 33i
+ 27j - 39k;
n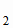 = ( 11; 9; -13).
= ( 11; 9; -13).
С помощью формулы (1.9) найдем косинус угла между плоскостями:
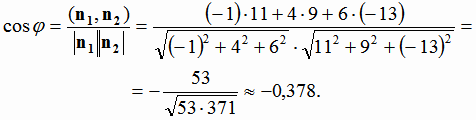
Знак "минус" показывает, что мы нашли косинус тупого угла между плоскостями. Косинус дополнительного ему острого угла
равен 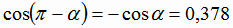 . В ответе договоримся писать положительное значение косинуса, т.е. косинус острого угла.
. В ответе договоримся писать положительное значение косинуса, т.е. косинус острого угла.
Ответ: 0,378.
Задача 2. Найдем координаты вектора 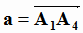 , который является направляющим вектором прямой
, который является направляющим вектором прямой
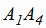 :
: 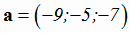 . Синус угла β между ребром A1A4 и плоскостью
. Синус угла β между ребром A1A4 и плоскостью
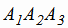 равен:
равен:
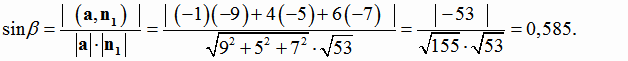
Ответ: 0,585.
Задача 3. Для нахождения площади грани 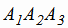 воспользуемся свойствами векторного произведения
векторов
воспользуемся свойствами векторного произведения
векторов 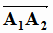 и
и 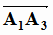 , найденного в задаче 1 (см. формулу (1.22) ) :
, найденного в задаче 1 (см. формулу (1.22) ) :
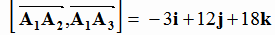 .
.
Тогда по формуле (1.5)
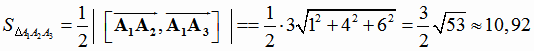
Ответ: 10,92
Задача 4. Объём пирамиды A1A2A3A4 равен 1/6 модуля смешанного
произведения векторов 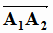 ,
, 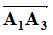 и
и 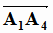 . Координаты первых двух векторов и их
векторного произведения уже вычислены - см. (1.22) , найдем
. Координаты первых двух векторов и их
векторного произведения уже вычислены - см. (1.22) , найдем
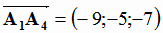 . Вычислим смешанное произведение:
. Вычислим смешанное произведение:
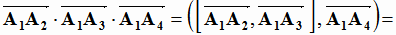
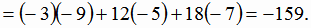
Тогда искомый объём равен: 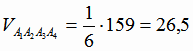 .
.
Ответ: 26,5.
Задача 5. Вычислим длину h высоты пирамиды тремя разными способами (рис.1.10)
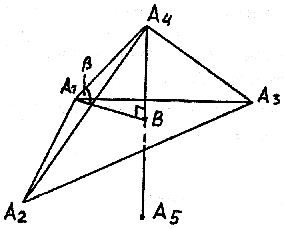
Рис. 1.10.
1. Из прямоугольного треугольника A1A4B найдем катет A1B, зная гипотенузу A1A4 и острый угол β (см. рис. 1.10):
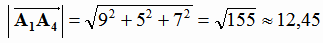 ,
,
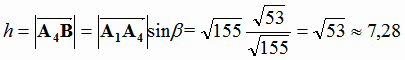
Заметим, что округление результата следует производить только на заключительном этапе, промежуточные выкладки необходимо выполнять с точными значениями переменных.
2. Используем объём пирамиды и площадь грани. Имеем:
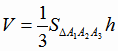 ,
,
откуда
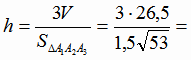
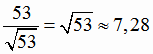
3. Вычислим h как расстояние от точки A4 до плоскости A1A2A3.. Уравнение этой плоскости найдем по формуле
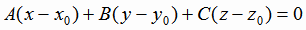 ,
,
где 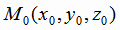 - координаты произвольной точки на плоскости, n = (A,B,C) - нормальный вектор к
плоскости. Нормальный вектор получен в задаче 1, формула (1.23); в качестве точки М
- координаты произвольной точки на плоскости, n = (A,B,C) - нормальный вектор к
плоскости. Нормальный вектор получен в задаче 1, формула (1.23); в качестве точки М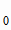 возьмем, например, точку А
возьмем, например, точку А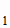 :
:
-1(x-9) + (y-4) + 6(z-4) = 0.
Или после упрощения:
| -x + 4y +6z -31 = 0 | (1.24) |
Расстояние h от точки
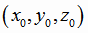 до плоскости, заданной уравнением Ax+ By+ Cz +D =0, вычисляется
по формуле (1.11):
до плоскости, заданной уравнением Ax+ By+ Cz +D =0, вычисляется
по формуле (1.11):
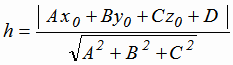
В нашем случае имеем:
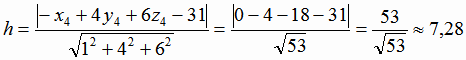
Поскольку результаты всех трех способов совпали, делаем вывод о правильности наших вычислений.
Ответ: 7,28.