Главная страница

    1 Теоретическое введение

    1.1 Оценка коэффициентов регрессии

    Важной задачей математической статистики является получение функциональной зависимости одной величины (y) от другой (х) по результатам эксперимента. Будем считать, что функциональная зависимость между величинами, называемая в дальнейшем моделью, известна из предварительных сведений с точностью до параметров 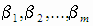и имеет вид

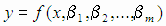(4.1)

    Для отыскания неизвестных параметров проведено n наблюдений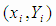, 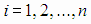. Но так как результаты наблюдений не свободны от погрешностей измерений, которые мы будем рассматривать как случайные ошибки, то по ним нельзя точно найти искомые параметры. Поэтому приходится ставить задачу об отыскании не значений параметров, а их оценок по результатам эксперимента.

    Будем предполагать, что значения аргументов 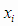известны точно, а значения функции 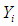- взаимно независимые случайные величины, включающие случайные ошибки 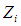, т.е.

,

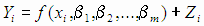где

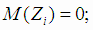
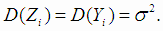
    Здесь мы предполагаем, что измерения равноточны. Для оценок параметров 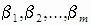используется метод наименьших квадратов. В качестве оценок этих параметров принимаются значения 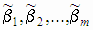, при которых имеет минимум функция (МНК-оценки)

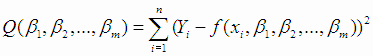(4.2)

    Уравнение (4.1) называется уравнением регрессии, а отыскание оценок параметров и исследование получаемых моделей - регрессионным анализом.

    Будем рассматривать уравнения регрессии, линейные относительно оцениваемых параметров :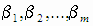

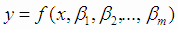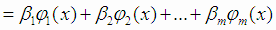(4.3)

    Функции называются базисными функциями, их рассматривают на множестве точек 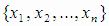, где n - число экспериментов. Функция Q (4.2) в этом случае запишется в виде:

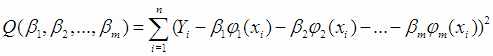(4.4)

    Для нахождения минимума найдем частные производные функции 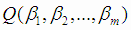по переменным 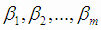и приравняем их к нулю (необходимые условия минимума функции). Получим систему уравнений:

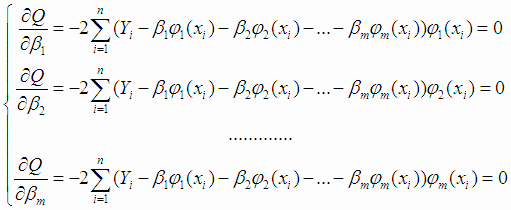
которую после преобразований можно записать в виде:

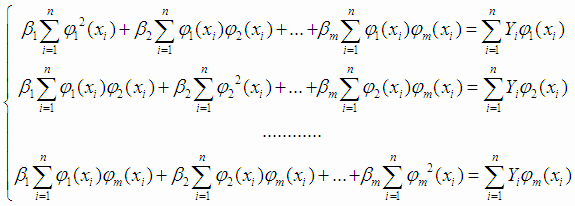(4.5)

    Следовательно, оценки параметров 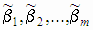являются решениями линейной алгебраической системы m уравнений (4.5).

    Введем обозначения:

; ,

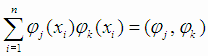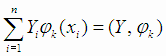тогда система (4.5) запишется в виде:

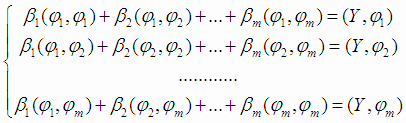
    С использованием следующих матричных обозначений:

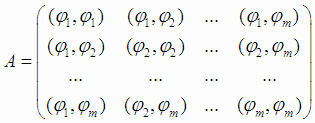- матрица коэффициентов при неизвестных,

- вектор правых частей, 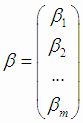- вектор параметров,

    Система (4.5) принимает вид

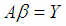(4.6)

    При условии, что А - невырожденная матрица, решение системы (4.6) можно записать в виде

,

(4.7)

где 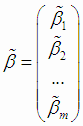- вектор МНК-оценок параметров регрессионной модели (4.3).

    Оценки параметров линейной регрессии, получаемые по методу наименьших квадратов, имеют следующие свойства:

    1. Они являются линейными функциями результатов наблюдений 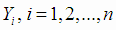, и несмещенными оценками параметров, т.е.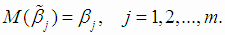

    2. Они имеют минимальные дисперсии в классе несмещенных оценок, являющихся линейными функциями результатов наблюдений.

Следующая страница