Главная страница Предыдущая страница
1.6 Числовые характеристики дискретных случайных величин
Случайные величины могут описываться числовыми характеристиками, среди которых различают характеристики положения (математическое
ожидание, мода, медиана) и характеристики рассеяния (дисперсия, среднеквадратическое отклонение).
Математическое ожидание 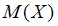 представляет собой среднее ожидаемое значение случайной величины.
Если пространство элементарных исходов состоит из конечного числа взаимно исключающих друг друга возможных исходов ω
представляет собой среднее ожидаемое значение случайной величины.
Если пространство элементарных исходов состоит из конечного числа взаимно исключающих друг друга возможных исходов ω 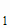 ,
ω
,
ω 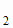 , ..., ω
, ..., ω 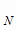 с вероятностями Р(ω
с вероятностями Р(ω 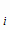 )=p
)=p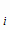 (i = 1, 2,..., N;
(i = 1, 2,..., N; 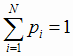 ), то математическое ожидание случайной величины Х = Х(ω
), Х(ω i) = xi, вычисляют по формуле:
), то математическое ожидание случайной величины Х = Х(ω
), Х(ω i) = xi, вычисляют по формуле:
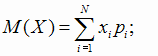 , , |
(1.18) |
Свойства математического ожидания:
1) 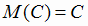 , где С = const,
, где С = const,
2) 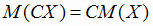 ,
,
3) 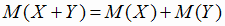 для любых случайных величин Х и Y,
для любых случайных величин Х и Y,
4) 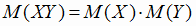 если Х и Y независимы.
если Х и Y независимы.
Таким образом, если случайная величина Х представлена в виде линейной комбинации величин Х1,
Х2, ..., ХL, то её математическое ожидание вычисляют по свойству линейности:
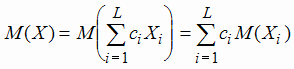 . . |
(1.19) |
Если известна таблица распределения дискретной случайной величины, то математическое ожидание любой её функции может быть
вычислено по формуле:
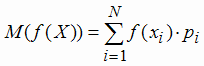 . . |
(1.20) |
Для характеристики степени разбросанности значений случайной величины около её математического ожидания 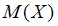 =
а вводятся понятия дисперсии
=
а вводятся понятия дисперсии 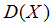 и среднего квадратического отклонения
и среднего квадратического отклонения 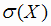 по формулам:
по формулам:
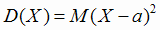 ; ; 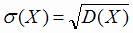 |
(1.21) |
Свойства дисперсии и среднего квадратического отклонения:
1) 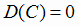 ;
; 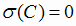 , где С = const,
, где С = const,
2) 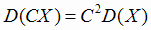 ;
; 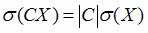 ,
,
3) 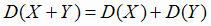 , если Х и Y независимы.
, если Х и Y независимы.
Дисперсия для дискретной случайной величины Х может быть найдена по формуле:
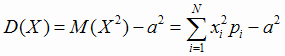 . . |
(1.22) |
Математическое ожидание и дисперсия дискретной случайной величины Х, имеющей биномиальное распределение,
могут быть найдены по формулам:
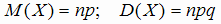 , , |
(1.23) |
где р - вероятность того, что событие А произойдет, q - вероятность того, что событие А не произойдет в каждом
из независимых испытаний.
Следующая страница
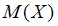 представляет собой среднее ожидаемое значение случайной величины.
Если пространство элементарных исходов состоит из конечного числа взаимно исключающих друг друга возможных исходов ω
представляет собой среднее ожидаемое значение случайной величины.
Если пространство элементарных исходов состоит из конечного числа взаимно исключающих друг друга возможных исходов ω 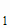 ,
ω
,
ω 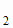 , ..., ω
, ..., ω 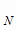 с вероятностями Р(ω
с вероятностями Р(ω 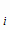 )=p
)=p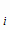 (i = 1, 2,..., N;
(i = 1, 2,..., N; 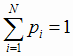 ), то математическое ожидание случайной величины Х = Х(ω
), Х(ω i) = xi, вычисляют по формуле:
), то математическое ожидание случайной величины Х = Х(ω
), Х(ω i) = xi, вычисляют по формуле: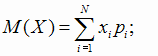 ,
, 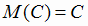 , где С = const,
, где С = const,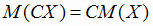 ,
,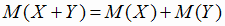 для любых случайных величин Х и Y,
для любых случайных величин Х и Y,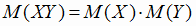 если Х и Y независимы.
если Х и Y независимы.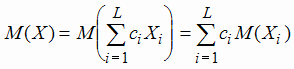 .
. 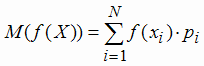 .
. 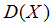 и среднего квадратического отклонения
и среднего квадратического отклонения 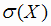 по формулам:
по формулам: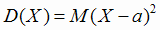 ;
; 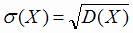
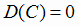 ;
; 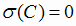 , где С = const,
, где С = const,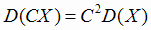 ;
; 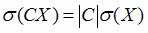 ,
,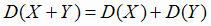 , если Х и Y независимы.
, если Х и Y независимы.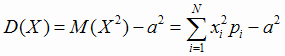 .
. 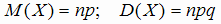 ,
,