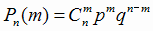 ,
,Главная страница Предыдущая страница
1.5 Биномиальное распределение дискретной случайной величины
Пусть проводится n независимых испытаний, в каждом из которых событие А наступает с вероятностью р (0 < p < 1), и не наступает с вероятностью q, q = 1 - p. Обозначим Pn(m) - вероятность того, что в n испытаниях событие А наступит ровно m раз, тогда случайная величина Х такая, что Р(Х=m) = Pn(m) определяет биномиальное распределение или распределение Бернулли. Вероятности Pn(m) вычисляются по формуле:
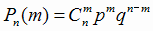 , , |
(1.16) |
где коэффициенты 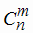 называются числом сочетаний из n элементов по m и вычисляют по формуле:
называются числом сочетаний из n элементов по m и вычисляют по формуле:
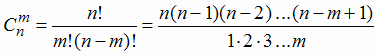 |
(1.17) |
Из формулы (1.17) видно, что 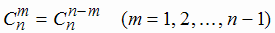 .
.
По определению полагают также 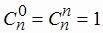 .
.
Рассмотрим смысл коэффициентов 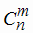 . Пусть заданы n разных элементов. Всевозможные
группировки из данных n элементов по m элементов в каждой, отличающиеся друг от друга хотя бы одним элементом, при этом порядок
расположения элементов в группировке безразличен, называются сочетаниями из n элементов по m. Например, n = 4, имеем
4 элемента: а, b, c, d. Выпишем сочетания из четырех элементов по два: ab, ac, ad, bc,
bd, cd. Из определения следует, что сочетания ab и ba не различимы. Число таких сочетаний и находится по формуле
(1.17),
. Пусть заданы n разных элементов. Всевозможные
группировки из данных n элементов по m элементов в каждой, отличающиеся друг от друга хотя бы одним элементом, при этом порядок
расположения элементов в группировке безразличен, называются сочетаниями из n элементов по m. Например, n = 4, имеем
4 элемента: а, b, c, d. Выпишем сочетания из четырех элементов по два: ab, ac, ad, bc,
bd, cd. Из определения следует, что сочетания ab и ba не различимы. Число таких сочетаний и находится по формуле
(1.17), 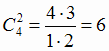 .
.
Примеры вычисления:
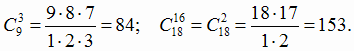
Вероятность того, что в n испытаниях событие А наступит менее m раз, равна сумме вероятностей:
Pn(0) + Pn(1) + ... + Pn(m - 1);
более m раз - сумме вероятностей:
Pn(m + 1) + ... + Pn(n)
Часто расчёты упрощаются, если применять свойство вероятностей Рn(m)
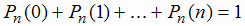
Пример 1.10. В урне 10 шаров, из них 3 белых. Вынимают наугад 3 шара. Найти распределения вероятностей случайной величины Х - числа вынутых белых шаров при повторной выборке. При повторной выборке после каждого извлечения шара отмечают его цвет и возвращают шар в урну, снова перемешивая шары.
Решение: P (X = 0) = Р(три раза вынимали черный шар) = 0,7· 0,7· 0,7 , где 0,7 - вероятность вынуть черный шар из урны. Так как после каждого извлечения шар возвращают в урну и шары перемешивают, то система шаров возвращается в исходное состояние и вероятность вынуть черный шар одинакова при любом извлечении.
P (X = 1) = Р (вынимали один белый шар и два черных) = Р (вынули белый шар первым или вынули белый шар вторым, или вынули белый шар третьим) =
= 0,3· 0,7· 0,7+0,7· 0,3· 0,7+0,7· 0,7· 0,3 =3 · 0,3 · 0,72 = 0,441.
P (X = 2) = Р (вынимали один черный шар и два белых) = Р (вынули черный шар первым или вынули черный шар вторым, или вынули черный шар третьим) =
= 0,7· 0,3· 0,3+0,3· 0,7· 0,3+0,3· 0,3· 0,7 = 3 · 0,32 · 0,7 = 0,189.
P (X = 3) = Р(три раза вынимали белый шар) = 0,3· 0,3· 0,3.
Распределение вероятностей случайной величины Х представлено в таблице 1.2.
Таблица 1.2
| Х | Р |
| 0 | 0,73 = 0,343 |
| 1 | 3 · 0,3 · 0,72 = 0,441 |
| 2 | 3 · 0,32 · 0,7 = 0,189 |
| 3 | 0,33 = 0,027 |
| Σ | 1,000 |