Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Двухмерная задача теплопроводности с различными условиями теплоотдачи по периметру сечения металла при прокатке

    В ходе технологического процесса прокатки теплоотдача на различных участках поверхности раската существенно изменяется из-за контакта металла с инструментом (валками, проводками, роликами рольганга), охлаждения воздухом и водой, наличия окалины. Это существенно влияет на температурное поле металла и должно быть учтено в температурных расчётах.

    В данной постановке рассматривается плоская температурная задача для сечения проката произвольной формы. Температура металла T(x,y,t) в точке с координатами x, y поперечного сечения тела в момент времени t вычисляется по известному начальному распределению температуры

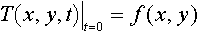
и условиям теплообмена с окружающей средой с использованием краевых условий третьего рода.

    Вычисления реализуют интегрирование уравнения теплопроводности:

,

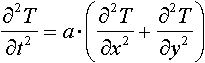(1)

при краевом условии

,

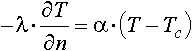где T - температура в соответствующей точке контура;

    a - коэффициент температуропроводности;

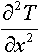    - вторая производная по х - изменение теплового потока по оси х;

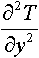    - изменение теплового потока по оси у;

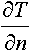    - производная по нормали к поверхности;

    α - коэффициент теплоотдачи от поверхности в окружающую среду;

    T_c - температура окружающей среды;

    c - удельная теплоёмкость единицы массы вещества как функция химического состава материала и температуры;

    ρ - плотность вещества как функция химического состава материала, температуры и координат;

    λ - коэффициент теплопроводности как функция химического состава материала и температуры;

    Метод сеток рассматривает вычисляемую функцию в узлах с номерами j,i в дискретные моменты времени t_con.

    Для перехода от дифференциальных уравнениям к конечным используем приближенные соотношения - разделённые (конечные?) разности вместо производных:

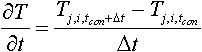
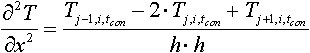(2)

,

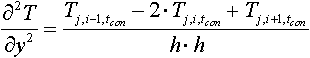где h - шаг сетки.

    Подстановка (2) в уравнение (1) дает правило (явная разностная схема) для вычисления значений температуры в текущем внутреннем узле в следующий момент времени.

    Граничное условие - это тепловой баланс для приграничного узла. Разностные уравнения для вычисления температуры в узле через температуры соседних внутренних узлов и с учётом теплоотдачи наружу следует в общем виде записывать с логическими функциями результатов распознавания принадлежности узла с суммированием по четырём соседним узлам:

,

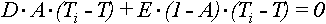где A=1 - признак принадлежности узла внутренности области (A=1) и внешней области (A=0);

;

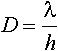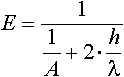
    Для реализации возможности решения температурной задачи при различных условиях теплоотдачи по периметру сечения коэффициент теплоотдачи считается известной функцией координаты точки на поверхности и расчётной температуры в этой же точке. Получены аналитические выражения для определения коэффициента теплоотдачи при охлаждении на воздухе, в масле, в воде, а также при непосредственном контакте металла с инструментом при горячей прокатке.

    Шаг по времени Δt для устойчивости вычислений не должен превышать некоторого значения, имеющего не только математическое, но и физическое объяснение - это шаг, при котором вычисляемая температура в узле становится равновесной с температурой смежных элементов - соседних узлов.

    Разработанный алгоритм определения изменений температурного поля по сечению раската может быть применён в расчётах технологических процессов производства плоского проката, сортовых и фасонных профилей.