 |
Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru |
| На главную | Контакты | Выполнить расчёт (запустить приложение) |
|
|||
|
Расчёт сопротивления металла деформации с учётом истории нагружения
Для определения сопротивления металла деформации может быть использован аналитический метод, позволяющий для стали или сплава определенного химического состава и исходного состояния рассчитывать сопротивление металла деформации с учётом изменяющихся во времени технологических параметров - температуры, скорости, степени деформации, а также структурных упрочнений [524, 507, 508].
Метод расчёта сопротивления металла деформации основан на применении в расчётах кривой предельного упрочнения, представляющей собой зависимость сопротивления деформации от обжатия в случае отсутствия разупрочнения.
Кривая предельного упрочнения, за исключением участка упругости при данной температуре описывается зависимостью [1129]:
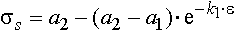 , , |
(1) |
где σs - сопротивление деформации;
a1, a2 - соответственно минимальное
и максимальное значения сопротивления деформации при данной температуре;
k1 - коэффициент, зависящий от химического состава стали;
ε - логарифмическая деформация.
Для учёта разупрочнения в формулу (1) будем подставлять не истинную деформацию ε, а условную εу. Последняя равна деформации, обеспечивающей получение такого же значения сопротивления деформации, но при отсутствии разупрочнения, т.е. характеризует упрочнение [1046]. Тогда формула (1) принимает вид
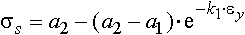 |
(2) |
Деформацию упрочнения εу следует рассматривать как разность между истинной деформацией ε и той частью деформации εр, которая не оказывает влияния на механические свойства стали в связи с протеканием процессов разупрочнения (в дальнейшем изложении будем называть её разупрочнением) εу=ε-εр, или в дифференциальной форме:
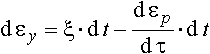 , , |
(3) |
где ξ - скорость деформации;
t - время.
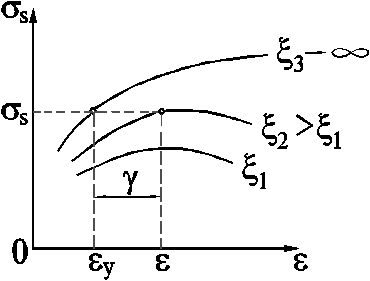
Рис. Схема к выводу формул для расчёта сопротивления деформации
Как показал анализ экспериментальных данных, разупрочнение в значительной степени зависит от величины деформации - при малых степенях происходит лишь незначительное устранение дефектов, тогда как после достижения определенной величины (при достаточном нагреве) интенсивность разупрочнения резко возрастает. Такой вид связи между деформацией и разупрочнением с некоторым приближением можно выразить квадратичной зависимостью. Выбор вида функции dεр/dt обусловлен стремлением достигнуть наиболее полного соответствия поведения функции физической природе процесса. Немаловажным фактором при выборе вида функции является также реальная возможность аналитического решения получаемого дифференциального уравнения.
Таким образом, скорость разупрочнения dεр/dt будем считать пропорциональной квадрату условной деформации, характеризующей достигнутое упрочнение
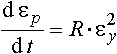 ,
,
где R - коэффициент разупрочнения.
Тогда формула (3) принимает вид
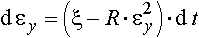 |
(4) |
При постоянной скорости деформации дифференциальное уравнение (4) имеет следующее решение:
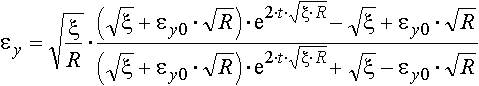 , , |
(5) |
здесь εу0 - начальное значение деформации упрочнения (при t=0).
Если εу0=0, то выражение (5) может быть преобразовано к виду
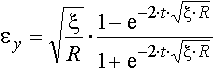 |
(6) |
В том случае, когда скорость деформации изменяется во времени, необходимо разбить процесс деформирования на участки, на которых скорость деформации можно считать постоянной. Если это невозможно, уравнение (4) решается численным методом.
Когда скорость деформации равна нулю (например, в паузах между проходами), уравнение (4) упрощается:
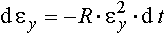
и его решение получается следующим:
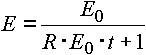 |
(7) |
Вычисленное по одной из формул (5), (6) или (7) значение деформации упрочнения подставляется в выражение (2). Таким образом, мы получили зависимость сопротивления деформации от величины и скорости деформации (от времени).
Выразим зависимость коэффициентов a, b и R от температуры. Исходя из физического смысла, можно утверждать, что а и b монотонно уменьшаются с увеличением температуры, поэтому аппроксимируем их полиномом второй степени:
a=k2+k3·Т+k4·T2
b=k5+k6·Т+k7·T2,
где Т - температура.
Коэффициент R характеризует интенсивность протекания процессов разупрочнения и может быть представлен функцией вида
R=k8[π/2+arctgk9·(T+k10)].
Представляется возможным учесть структурные упрочнения. В случае расчёта сопротивления металла деформации при температурах ниже температуры фазового превращения для учёта фазового наклепа при переходе через температуру, численно равную коэффициенту k11, к деформации упрочнения E прибавляется коэффициент k12:
E=E0+k12, при T<k11<T+ΔT
Коэффициенты k1-k12 для конкретного материала могут быть рассчитаны по опытным данным с использованием метода наименьших квадратов.
Таким образом, описанная методика позволяет рассчитывать сопротивление деформации в любой момент времени с учётом температуры, скорости и степени деформации, изменяющихся во времени.
В работе [1046] по литературным данным для расчёта сопротивления деформации с учётом истории нагружения определены коэффициенты k1 - k12, характеризующие особенности поведения материала в процессах упрочнения и разупрочнения, для сталей У10А [1055], Х18Н9Т [1099], 16MnCr5, 100Cr6, С45, X8CrNiTi1810 и C15 [1098]. В табл. 2 приведены средние отклонения расчётных значений сопротивления деформации от экспериментальных и указаны интервалы, в которых изменяются температура, скорость и степень деформации.
Таблица 2
Сравнение результатов расчёта сопротивления деформации по предлагаемой методике с экспериментальными данными
| Марка стали | Интервалы изменения определяющих параметров | Среднеквадратичные отклонения от задаваемых значений, % | |||||
| температура, °С | скорость деформации, с | степень деформации | |||||
| минимальная | максимальная | минимальная | максимальная | минимальная | максимальная | ||
| У10А | 20 | 1457 | 0,0005 | 120 | 0,1054 | 0,6933 | 11,37 |
| Х18Н9Т | 900 | 1200 | 0,05 | 150 | 0,1 | 0,3 | 8,55 |
| 16MnCr5 | 20 | 1200 | 1,5 | 100 | 0,1 | 0,6 | 6,56 |
| 100Cr6 | 20 | 1100 | 0,1 | 90 | 0,1 | 0,5 | 11,77 |
| С45 | 20 | 1100 | 0,1 | 90 | 0,1 | 0,5 | 11,02 |
| X8CrNiTi1810 | 20 | 1100 | 0,1 | 90 | 0,1 | 0,5 | 12,50 |
| С15 | 20 | 1100 | 0,1 | 90 | 0,1 | 0,5 | 12,49 |
Полученные значения среднеквадратичных отклонений в широком диапазоне изменений параметров деформации и температуры указывают на удовлетворительную сходимость результатов расчёта с экспериментальными данными.