Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Определение параметров методом прямого поиска

    Задача оптимизации предусматривает поиск условий, обеспечивающих экстремальное значение некоторого функционала. Определение параметров или коэффициентов, входящих в некоторую зависимость, обеспечивающих минимум отклонения расчётных значений от заданных, является частным случаем задачи оптимизации. При использовании метода наименьших квадратов в качестве критерия ошибки служит сумма квадратов отконений заданных и полученных значений для всех вариантов.

    Реализация основного положения метода наименьших квадратов для поиска коэффициентов, входящих в некоторую функцию, представляет собой решение системы дифференциальных уравнений в частных производных. Если функция представляет собой линейную комбинацию коэффициентов, то система дифференциальных уравнений преобразуется в систему линейных уравнений и вычисление коэффициентов практически не вызывает трудностей. К таким функциям относятся прежде всего полиномы, в также ряд других, например, показательная, которые могут быть преобразованы к линейной комбинации коэффициентов. Eсли зависимость имеет сложный вид, получить линейную систему уравнений не представляется возможным.

    Данная программа и предназначена для определения коэффициентов в таких зависимостях.

    Определение коэффициентов производится с помощью метода наименьших квадратов, согласно которому достигается условие минимума критерия, в нашем случае - относительного среднеквадратического отклонения расчётных значений функции от задаваемых данных, вычисляемого по формуле

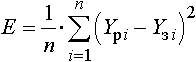
где n - число заданных значений функции;
    Y_зi,Y_рi - соответственно заданное и расчётное значения функции в i-ой строке.

    Одним из наиболее надежных методов прямого поиска экстремума критерия является метод конфигураций [359], который реализуется следующим образом.

    Изменяется начальное значение одного из коэффициентов на величину шага dX_j и находится относительное среднеквадратическое отклонение E. Если оно получилось больше имеющегося минимального отклонения E_min, то возвращаемся к исходному значению коэффициента и меняем знак шага на противоположный.

    Таким образом поступаем с каждым коэффициентом. После изменения последнего коэффициента вновь переходим к первому.

    Если при изменении коэффициентов в сторону увеличения и уменьшения значение минимального среднеквадратического отклонения не изменяется, то для каждого коэффициента уменьшаем шаг. Расчёт прекращаем в том случае, когда изменение коэффициентов на заданную величину погрешности не приводит к уменьшению относительного среднеквадратического отклонения.