Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Площадь контакта металла с валками при прокатке в калибрах

    При прокатке в калибрах, когда обжатие полосы по ширине калибра распределяется неравномерно, поверхность контакта полосы с валками имеет сложное очертание. Если начало координат расположить на средней линии валков, уравнение контактной поверхности можно представить в следующем виде [1082]:

,

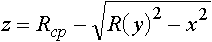где x, y, z  - координаты точки контактной поверхности по длине, ширине и высоте очага деформации;
   R_ср - средний радиус валков;
   R(y) - текущий радиус валка при изменении координаты y в пределах

,

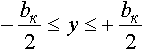здесь b_к - ширина калибра.

    Координата x в зависимости от координаты y изменяется в пределах

0≤x≤l_д(y),

где l_д(y) - длина очага деформации в продольном сечении при соответствующей координате y, изменяющейся по ширине калибра.

    Длина очага деформации в продольном сечении:

,

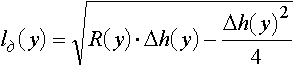где Δh(y) - функция распределения абсолютного обжатия по ширине калибра.

    Площадь контактной поверхности полосы с одним из валков определяется выражением:

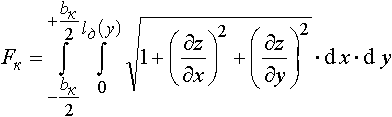
    Фактическое значение площади контактной поверхности используется при расчётах работы или мощности сил трения скольжения, при расчётах процессов теплообмена в очаге деформации. При расчётах усилия и крутящего момента прокатки пользуются величиной площади горизонтальной проекции контактной поверхности:

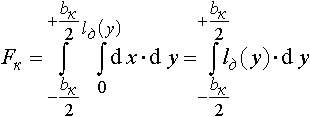
    При прокатке в простых калибрах в случае равенства катающих диаметров обоих валков процесс деформации проходит симметрично, контактные поверхности на обоих валках будут одинаковы. На рис. 66 показана форма горизонтальной проекции контактной поверхности при некоторых схемах прокатки.

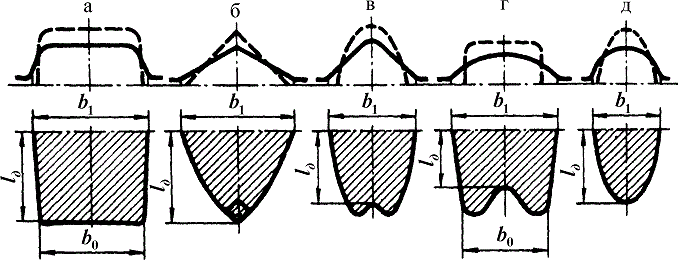
Рис. 66. Форма горизонтальной проекции контактной поверхности при прокатке по схемам:
а - прямоугольник-ящичный калибр; б - квадрат-ромб (ромб-ромб, ромб-квадрат); в - овал-квадрат; г - квадрат-овал; д - овал-круг

    В ящичных калибрах (рис. 66, а) форма контактной поверхности близка к равнобедренной трапеции с основаниями b₀ и b₁ и высотой, равной длине очага деформации по дну калибра l_д. При прокатке в системах калибров ромб-квадрат, ромб-ромб (рис. 66, б) контактная поверхность имеет форму равнобедренного треугольника с основанием b₁ и выпуклыми наклонными сторонами, причем в зависимости от радиусов скругления углов калибра и заготовки вершина контактной площади может быть острой, плоской или слегка вогнутой. Форма контактной поверхности при прокатке в квадратном калибре овальной заготовки показана на рис. 66, в. Вогнутость контура контактной поверхности по месту, соответствующему вершине калибра, будет тем больше, чем больше притупление вершины задаваемого овала. При прокатке в овальном калибре квадратной заготовки в вершине калибра имеют место минимальное обжатие и минимальная длина очага деформации l_д, что обусловливает получение контактной поверхности формы, показанной на рис. 66, г. В овальных и круглых калибрах при обжатии овальных заготовок контактная поверхность имеет очертания полуэллипса с малой осью b₁ и большой полуосью l_д (рис. 66, д).

    При прокатке металла в калибрах, например при прокатке круга, овала, квадрата на ребро, уголков и других, контактная поверхность определяется графически, аналитически или графо-аналитически.

    Аналитически площадь контакта определяется методами приведенной или соответственной полосы. По методу приведенной полосы Δh принимается равным среднему линейному обжатию по ширине профиля:

,

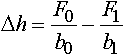где F₀ и F₁ - площади сечения профиля до и после прокатки соответственно.

    Катающий радиус R_к принимается равным

,

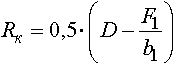где D - диаметр валка.

    Пользуясь этим методом, Δh рассчитывается по формулам (рис. 72):

    для ромба, прокатываемого из ромба,

Δh=A₁·(h₀-h₁);

    для овала, прокатываемого для квадрата,

Δh=h₀-0,7·h₁

Δh=h₀-0,85·h₁;

    для квадрата, прокатываемого из овала,

Δh=A₂·h₀-A₃·h₁;

    для круга

Δh=0,85·h₀-0,79·h₁,

где A₁, A₂, A₃ - коэффициенты.

    В этих формулах рекомендуется принимать коэффициенты A₁=0,55-0,6, A₂=0,65-0,7, A₃=0,55-0,6.

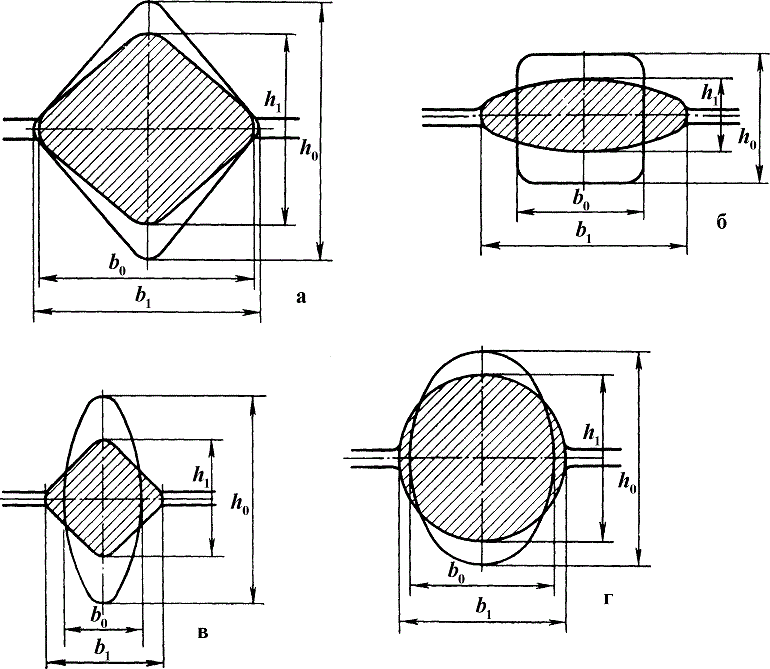
Рис. 72. Схемы обжатия при прокатке:
а - ромб; б - овал из квадрата; в - квадрат из овала; г - круг из овала

    Площадь горизонтальной проекции контактной поверхности для рассмотренных схем прокатки достаточно точно определяется по формулам В.Г. Дрозда, полученным аналитическим методом:

F_к=0,67·b₁· l_д (ромб-ромб, ромб-квадрат, квадрат-ромб);

F_к=0,54·(b₀+b₁)·l_д (квадрат-овал);

F_к=0,75·b₁·l_д (овал-квадрат, овал-овал, овал-круг, круг-овал).

    Результаты расчёта по приведенным формулам на 2-9 % превышают результаты определения площади контакта графическим методом.

    В литературе имеются более точные формулы, предложенные В.К. Смирновым, В.А. Шиловым, Ю.В. Инатовичем, учитывающие влияние на контактную площадь отношения осей калибра и заготовки, степени заполнения калибра и других факторов.

    Площадь горизонтальной проекции контактной поверхности при прокатке в калибрах можно также определить графическим или графо-аналитическим способами. Эти способы дают погрешность ~5-6 % . Особенно целесообразно использовать эти способы для определения контактной площади при прокатке в фасонных калибрах.

    При графическом способе вычерчивается в трех проекциях калибр вместе с находящейся в нём прокатываемой полосой, наносятся линии пересечения валка с поступающей полосой (рис. 71) и определяется площадь соприкосновения.

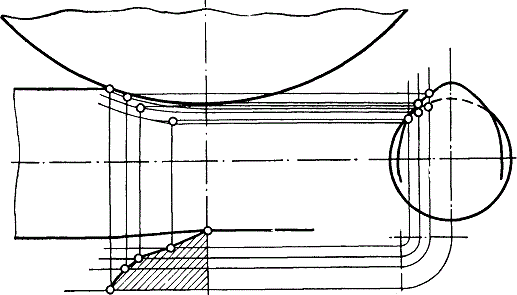
Рис. 71. Определение контактной площади графическим способом

    Для более точного подсчёта этой площади целесообразно вычерчивать калибр в увеличенном масштабе.

    Графо-аналитический метод разработан А.А. Динником. На чертеже в большом масштабе вычерчивается профиль калибра и поперечное сечение прокатываемой полосы, после чего вертикальными линиями профиль калибра и полосы делится на ряд элементов. Для каждого сечения графически в соответствии с заданным масштабом определяется величина обжатия Δh_i; величина радиуса в i-том сечении определяется расчётом исходя из действительного радиуса валка R_i с учётом масштабного коэффициента. Тогда для каждого сечения длина проекции дуги захвата:

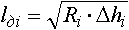
    Влияние уширения полосы учитывается путем соединения плавной кривой вершины задаваемой полосы с точкой, соответствующей максимальному уширению в конце дуги захвата.

    По вычисленным значениям l_д1, l_д2, l_д3, ..., l_дi и т.д. на горизонтальной проекции строится контур контактной поверхности и определяется её площадь, величина которой с помощью масштабных коэффициентов переводится в действительные числовые значения. Точность данного метода составляет 5-6 %.

    Рассмотрим некоторые особенности определения контактной площади в фасонных калибрах на примере прокатки уголкового профиля. На рис. 67 представлены в совмещенном виде профили калибра и прокатываемой полосы.

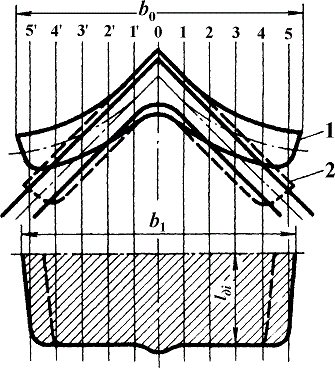
Рис. 67. Определение контактной площади графо-аналитическим методом:
1 - исходное положение заготовки; 2 - положение заготовки при обжатии в калибре

    При совмещении профилей необходимо учесть изгиб элементов заготовки при входе в калибр, а также правильно распределить обжатия между верхним и нижним валками. Положение заготовки в калибре выбирается таким, при котором обжатия верхним и нижним валками обеспечивают примерное равенство длины очага деформации в каждом вертикальном сечении со стороны верхнего и нижнего валков с учётом различия катающих радиусов верхнего R_в и нижнего R_н валков в каждом сечении. Используя графо-аналитический метод, в каждом i-том вертикальном сечении графически определяется величина обжатия Δh_i=Δh_в+Δh_н и рассчитывается длина очага деформации по формуле:

,

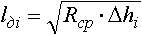где

R_ср=2·R_н·R_в/(R_н+R_в).

    После построения контура горизонтальной проекции контактной поверхности, путем планиметрирования, определяется её площадь с учётом масштаба построения. Можно заметить, что в некоторых сечениях (5,5') величину вертикального обжатия можно отнести только к одному (верхнему) валку. Это обусловливает некоторое различие контактных поверхностей на верхнем и нижнем валках при прокатке в фасонных калибрах. В расчётах используется среднеарифметическое значение F_к на верхнем и нижнем валках.

    Для приближенного определения величины площади горизонтальной проекции контактной поверхности при прокатке в калибрах на практике широко используется метод приведенной полосы, который обычно дает несколько завышенные результаты (7-18 %). Площадь контакта определяется по формуле:

,

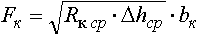где R_кср - средний катающий радиус валков;
    Δh_ср - среднее обжатие.

    Средний катающий радиус валков и среднее обжатие вычисляются по формулам:

R_к=(D_ср-h_1ср)/2;

,

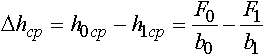где D_ср - средний диаметр валка;
   h_0ср - средняя высота исходного профиля (до прохода);
   h_1ср - средняя высота конечного профиля (после прохода).

    Использование этого метода для определения F_к в фасонных калибрах может привести к неправильным результатам из-за изгиба заготовки при входе в калибр. При этом значительно уменьшается ширина исходной заготовки и в расчётах h_0ср следует принимать b₀≈b₁.