Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Уширение при прокатке на гладкой бочке

    Для расчёта уширения при прокатке на гладкой бочке получено много зависимостей. В начале столетия уширение считали пропорциональным обжатию и длине геометрического очага деформации по формулам Л. Жеза [1001], С.Н. Петрова [1001] и Э. Зибеля [1001]. В дальнейших формулах учтено, что уширение пропорционально не всей дуге захвата, а только зоне опережения - формулы С.И. Губкина [1001] и Б.П. Бахтинова [1128].

    В последующем для аналитического определения уширения разными авторами предложены десятки различных формул, выведенных на основании эмпирических данных или некоторых теоретических допущений.

    Для определения величины свободного уширения в настоящее время пользуются формулами А.И. Целикова - А.И. Гришкова, А.П. Чекмарева [170], Б.П. Бахтинова, С.И. Губкина, М.С. Мутьева [1127] и другими, которые при прокатке на гладкой бочке дают удовлетворительное совпадение расчётных данных с опытными.

    В случае прокатки с натяжением полученное значение абсолютного уширения Δb А.И. Целиков предлагает умножать на коэффициент C_н.

    Ю.М. Чижиков в своей работе [360] приводит хронологию развития расчётных методов определения уширения при прокатке на гладкой бочке, а также дает некоторую оценку различным формулам.

    Простое сравнение свидетельствует о чрезвычайной пестроте данных, получаемых по различным формулам для одних и тех же условий. Например, на рис. 2 каждая кривая отвечает определенной формуле, по которой подсчитаны значения показателя уширения Δb/Δh при постоянной высоте h₁=const=10 мм при прокатке на стане дуо 400 мм, с обжатиями от 2 до 75 %. Здесь показатель уширения определяется по формуле:

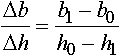
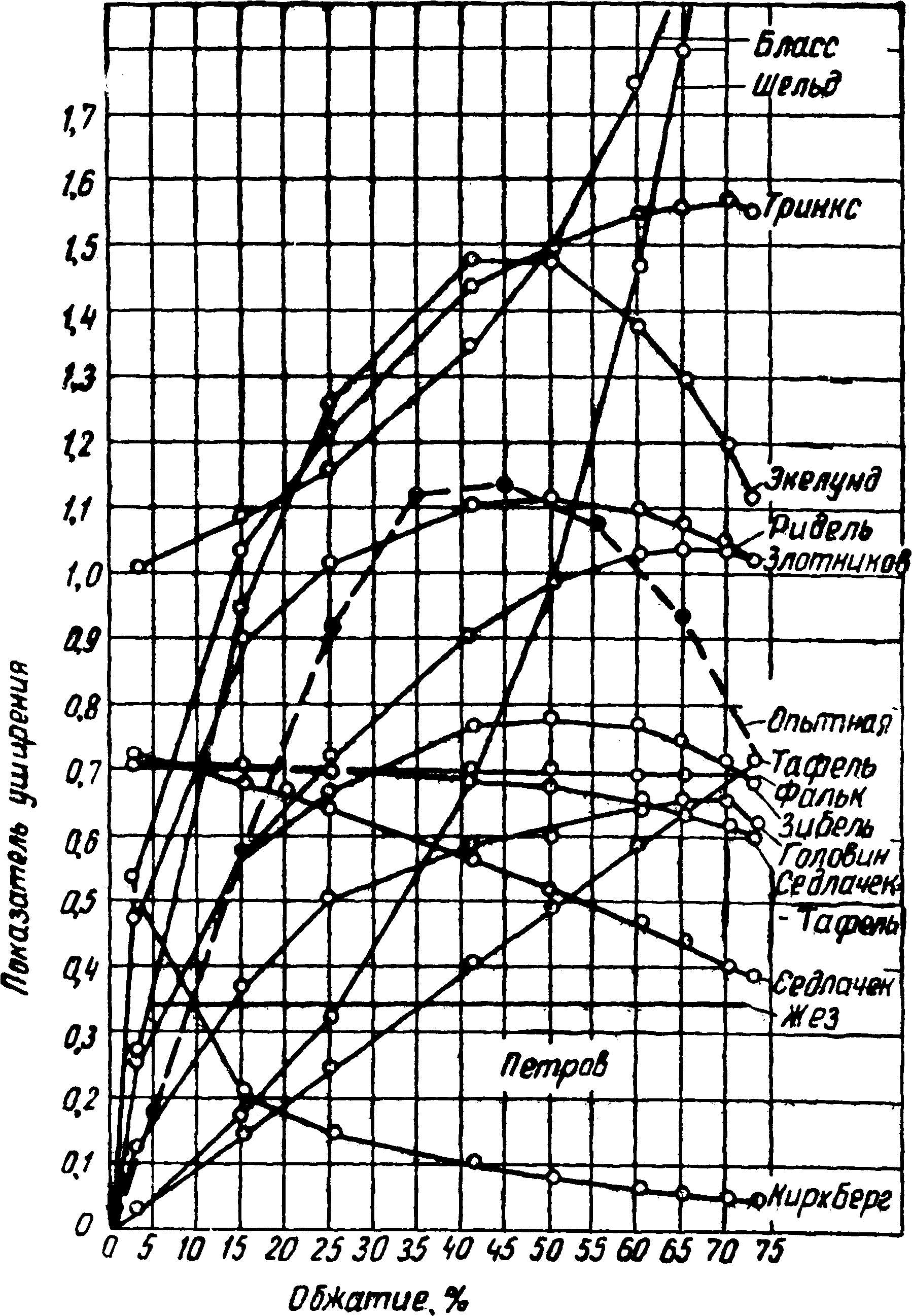
Рис. 2. Показатели уширения стали Ст1 при прокатке с обжатиями от 2 до 75 %,
рассчитанные по 15 формулам различных авторов

    Например, при обжатии 25 % при h₁=const показатель уширения лежит в очень широких пределах: от 0,15 до 1,28.

    По методу автора признаются достоверными такие формулы, которые качественно правильно отображают наиболее общие закономерности процесса прокатки, поскольку только качественно правильная формула может давать количественно верные результаты.

    Только соответствие любой формулы (теории) закономерностям практики, опыта является наиболее достоверным и объективным критерием пригодности их, поэтому закономерности, которые должны использоваться в качестве критерия, само собой разумеется, должны быть получены из опыта и иметь общий характер.

    Такими закономерностями, по мнению автора, являются:

    1) зависимость уширения от формы очага деформации, изменение которого характеризуется влиянием относительного обжатия при трех условиях, определяющих возможное изменение продольного сечения очага деформации (учитывающей и влияние трения);

    2) зависимость уширения от ширины полосы;

    3) зависимость уширения от диаметра валков.

    Эти закономерности, полученные из опыта, назовем действительными (истинными).

    В соответствии с предлагаемым методом анализа формул качественно правильными признаются такие формулы, которые в общих границах прокатки от Δh/h₀=0 до Δh/h₀=1 не входят в противоречие с действительными закономерностями.

    Исходя из этих основных положений, автор произвел исследование большинства из опубликованных формул для определения уширения при прокатке.

    К этим формулам относятся формула Бласса (1882 г.), Жеза (1900), Кирхберга (1905), Шельда (1910), Фалька (1910), Петрова (1917), Тафеля (1923), Седлачека (1924), Седлачека - Тафеля (1925), Экелунда (1927), Тринкса (1930), Зибеля (1930), Злотникова (1934), Головина 1934), Чихирова (1936), Риделя (1936), Александрова и Лашко (1936), Py (1939), Хейна (1941), Эсса (1943), Бахтинова (1946), Губкина (1947), Чекмарева (1948), Зарощинского (1949), Хейна (1949), Котеля (1950), Бехмана (1950), Тарновского (1952), Бахтинова (1953), Целикова (1953), Вусатовского (1953), Старченко (1958), Тарновского - Трубина (1958). Из всех рассмотренных формул наиболее правильно отображают действительный характер изменения уширения формулы Экелунда и Губкина.

    Для примера на рис. 3 показана зависимость показателя уширения от основных факторов прокатки, полученная вычислениями по формуле С.И. Губкина и на основании опытных данных.

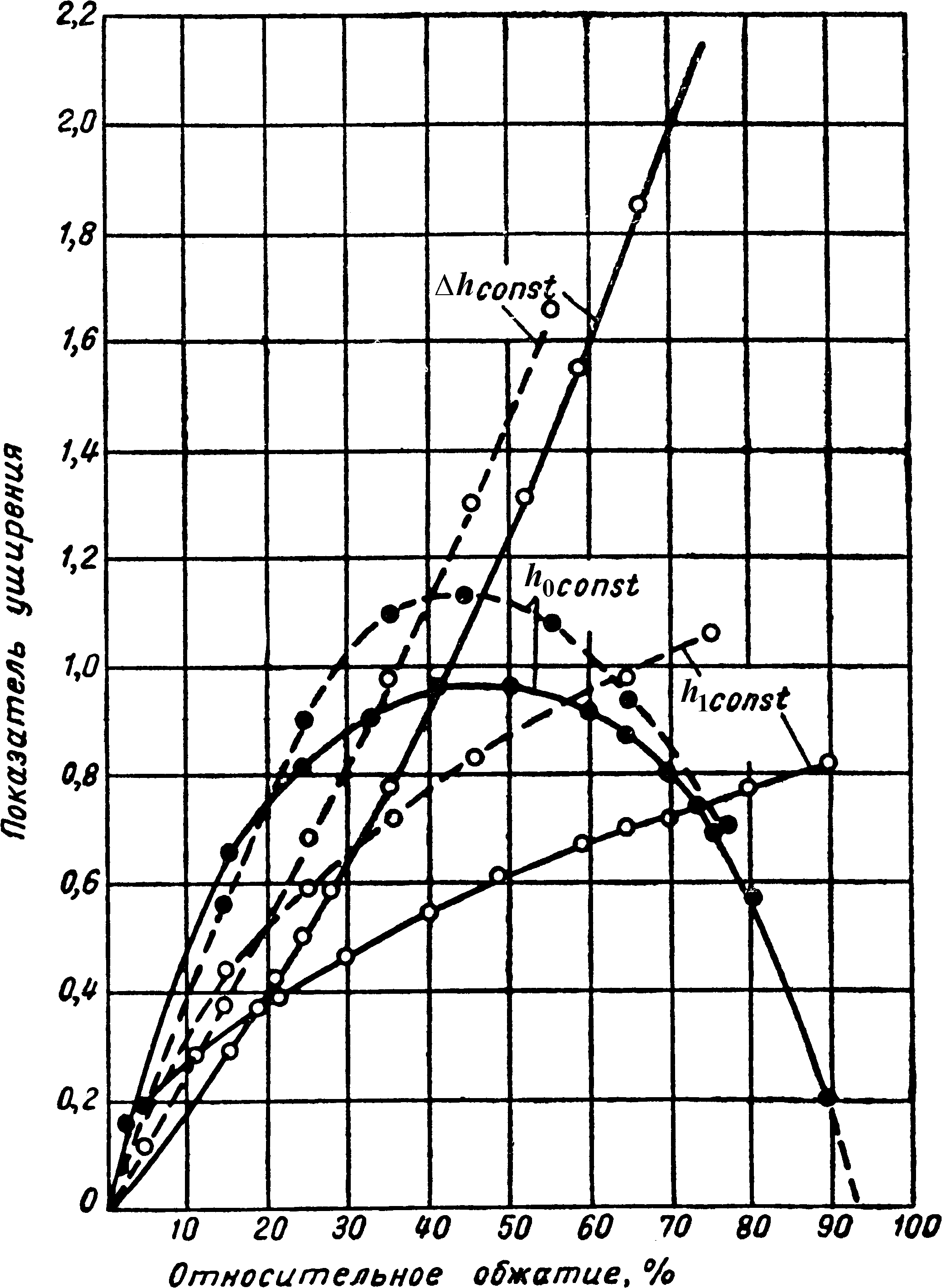
Рис. 3. Графический анализ формулы С.И. Губкина при Δh=7 мм, h₀=37 мм и h₁=10 мм постоянных (опытные кривые - штриховые)

    В заключение следует отметить, что, хотя по формулам С.И. Губкина и С. Экелунда получаются удовлетворительные результаты, их еще нельзя рассматривать как вполне пригодные для точных расчётов. Формулы следует проверить в широкой практике и уточнить постоянные коэффициенты, входящие в них.

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.