Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Решение системы линейных уравнений общего вида методом Гаусса с выбором главного элемента

    В данном разделе мы рассмотрим самый простой метод решения системы линейных уравнений. В курсе высшей математики системы линейных уравнений требуется решать как в виде отдельных заданий, например, «Решить систему по формулам Крамера», так и в ходе решения остальных задач. С системами линейных уравнений приходиться иметь дело практически во всех разделах высшей математики.

    Сначала немного теории. Что в данном случае обозначает математическое слово «линейных»? Это значит, что в уравнения системы все переменные входят в первой степени: x, y, z без всяких причудливых вещей вроде x², y², z², xyz и т.п., от которых в восторге бывают только участники математических олимпиад.

    В высшей математике для обозначения переменных используются не только знакомые с детства буквы x, y, z. Довольно популярный вариант - переменные с индексами: x₁, x₂, x₃. Либо начальные буквы латинского алфавита, маленькие и большие: a, b, c, A, B, C. Не так уж редко можно встретить греческие буквы - известные многим «альфа, бета, гамма». А также набор с индексами, скажем, с буквой «мю». Использование того или иного набора букв зависит от раздела высшей математики, в котором мы сталкиваемся с системой линейных уравнений. Так, например, в системах линейных уравнений, встречающихся при решении интегралов, дифференциальных уравнений традиционно принято использовать обозначения A, B, C.

    Рассматривается система линейных уравнений общего вида:

с матрицей коэффициентов А (m x m) и матрицей свободных членов R (m x n ), обе матрицы расположены по столбцам.

    Для решения системы используется метод исключения Гаусса с выбором главного элемента. Если матрица R - единичная, то решение Х равно обратной матрице A-1. Решение Х размещается на месте матрицы R.

   Данная система (1) представляется в матричном виде:

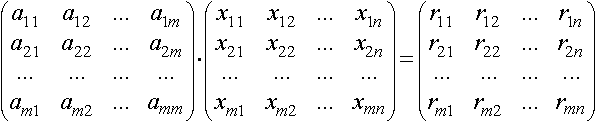(2)

    Матрица А исследуется на наибольший по абсолютной величине элемент. Пусть это a _ij, выберем его в качестве первого главного элемента (p = a_ij). Для того, чтобы контролировать потерю точности, образуем внутреннюю абсолютную погрешность с помощью a_ij и заданной относительной погрешности ε:

    Предположим, что a_{ij =} a₁₁. Если это не так, то поменяем местами первые строки матриц A и R с i -ми, и первый столбец матрицы А с j-ым. Кроме того, сохраняем информацию об обмене столбцов путем запоминания разности (j-1): индекса главного столбца j и счётчика шагов k = 1 (перестановка первого столбца с j-ым означает перестановку переменных x_l1 и x _lj, l = 1, 2, …, n.

    Теперь преобразуем элементы главных строк матриц A и R путем умножения на p-1. Остальные элементы - путем прибавления преобразованных первых строк этих двух матриц, умноженных на a_v1, к остальным v строкам. Таким образом, получим:

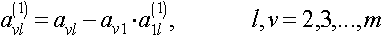
   Если информация об обмене столбцов запомнена на первом месте главной диагонали, то результатом первого шага являются две матрицы:

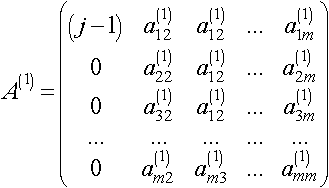
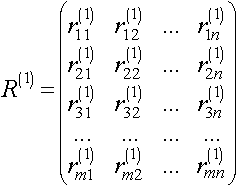
    Процесс повторяется m-2 раз, начиная на каждом шаге с матрицы А^(к) прежнего шага без первых К строк и первых К столбцов и с матрицы R^(k) без первых К строк. Результатом (m-1) шага являются матрицы:

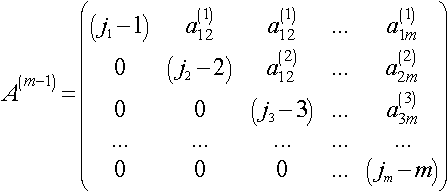
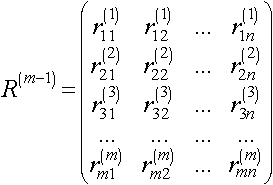
    Теперь вычисляем в обратном направлении и получаем:

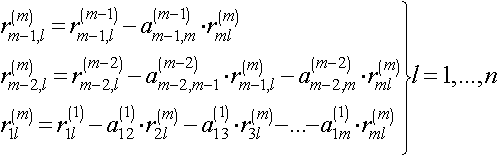
    После каждого шага обратной подстановки строки матрицы решения Х равной R^(m)должны быть переставлены согласно информации об обмене столбцов, содержащейся в соответствующем месте главной диагонали матрицы А^(m-1). Это нужно для того, чтобы получить правильную последовательность элементов столбцов r_vl^{( m)}, соответствующую последовательности элементов столбцов a_jv^(j).

   Существует единственный случай, при котором вышеописанный процесс нельзя применить для получения решения, когда на каком-нибудь шаге все элементы матрицы А^(k) становятся нулями и главный элемент не может быть найден. В этом случае процедура не выполняется и выдается сообщение об ошибке IER = -1. Фактически (вследствие ошибок округления) процедура выполняет дальнейшую проверку абсолютных значений главных элементов. Если на k -ом шаге исключения это абсолютное значение становится меньше, чем ε _l (см. уравнение (3)), то вероятно, что матрица А - особенная. Но, так как это необязательный случай, и так как эта проверка в большей степени зависит от выбора относительной погрешности ε, то процедура выдает только признак IER = K-I, показывающий, что в результатах, вычисленных по алгоритму возможна потеря точности. Например, ε =10^-5 и признак IER = 3 означают, что возможна потеря около пяти или более значащих цифр в исходных значениях 4-го шага исключения и, что матрица А, по-видимому, должна иметь ранг 3.

   В случае хорошо масштабированной матрицы А и подходящего выбора относительной погрешности, признак IER = K-I означает, что матрица А имеет ранг K-1.

   Если имеется только одно уравнение (m = 1), то проверка на потерю точности опускается.

    Форма выглядит следующим образом:

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.