 |
Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru |
| На главную | Контакты | Выполнить расчёт (запустить приложение) |
|
|||
|
Кривая (плотность вероятности) нормального распределения (Гаусса)
Норма́льное распределе́ние, также называемое распределением Гаусса или Гаусса-Лапласа - распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
\(f\left( x \right) = \frac{1}{{\sigma \sqrt {2\pi } }}e^{ - \frac{{\left( {x - \mu } \right)^2 }}{{2\sigma ^2 }}} \)
где параметр μ - математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ - среднеквадратическое отклонение (σ ² - дисперсия) распределения.
Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений.
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1.
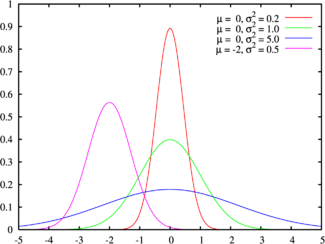
Зеленая линия соответствует стандартному нормальному распределению.
Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.