Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Уравнение прямой по 2 точкам

    Прямая - одно из основных понятий геометрии.

    При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

    Аналитически прямая задаётся уравнением (в трёхмерном пространстве - системой уравнений) первой степени.

    Общее уравнение прямой

    Общее уравнение линии на плоскости в декартовых координатах:

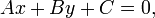
где A, B и C - произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

    При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде:

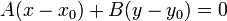
    Уравнение прямой с угловым коэффициентом

    Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось 0Y в точке (0, b) и образующая угол 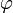с положительным направлением оси 0X:

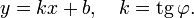
    Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси 0Y.

    Уравнение прямой в отрезках

    Прямая линия, пересекающая ось 0X в точке (a, 0) и ось 0Y в точке (0, b):

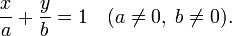
    В этом виде невозможно представить прямую, проходящую через начало координат.

    Форма выглядит следующим образом:

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.