Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Коэффициенты плоскости по заданным координатам 3-х точек

    Плоскость - одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

    Плоскость - алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

    Общее уравнение (полное) плоскости: Ax + By + Cz + D = 0,

где A, B, C и D - постоянные, причём A, B и C одновременно не равны нулю; в векторной форме:

(r, N) + D = 0,

где r - радиус-вектор точки M (x, y, z), вектор N = (A, B, C) перпендикулярен к плоскости (нормальный вектор).

    Направляющие косинусы вектора N:

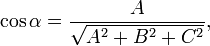
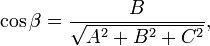
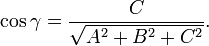
    Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При D = 0 плоскость проходит через начало координат, при А = 0(или В = 0, С = 0) плоскость параллельна оси 0Х (соответственно 0Y или OZ). При A = B = 0 (A = C = 0, или B = C = 0) плоскость параллельна плоскости 0XY(соответственно 0XZ или 0YZ).

    Уравнение плоскости, проходящей через три заданные точки М(x_i, y_i, z_i), не лежащие на одной прямой: ((r - r₁), (r₂ - r₁), (r₃ - r₁)) = 0 (смешанное произведение векторов), иначе:

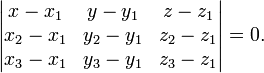
    Экранная форма для расчёта выглядит следующим образом:

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.