Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Коэффициенты параболы по заданным координатам 3-х точек

    Парабола (греч. парабола - приложение) - геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

    Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

    Уравнения

    Каноническое уравнение параболы в прямоугольной системе координат:

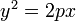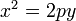    (или , если поменять оси)

    Квадратное уравнение 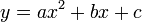при 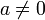также представляет собой параболу и графически изображается той же параболой, что и , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке А, координаты которой вычисляются по формулам:

,

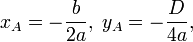где D = b² - 4ac - дискриминант

    Уравнение 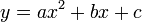может быть представлено в виде 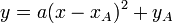, а в случае переноса начала координат в точку А каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим.

    Расчёт коэффициентов квадратного уравнения

    Если для уравнения известны координаты 3-х различных точек его графика (х₁;у₁), (х₂;у₂), (х₃;у₃), то его коэффициенты могут быть найдены так:

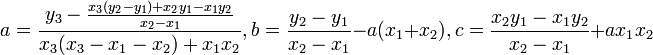
    Всё это нам уже хорошо известно из школьной алгебры, но всё равно, Вам в помощь, подскажу самый простой метод нахождения уравнения параболы по координатам трёх точек.

    Форма выглядит следующим образом:

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.