 |
Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru |
| На главную | Контакты | Выполнить расчёт (запустить приложение) |
|
|||
|
Тензорное исчисление
Тензорное исчисление, математическая теория, изучающая величины особого рода - тензоры, их свойства и правила действий над ними. Т. и. является развитием и обобщением векторного исчисления и теории матриц. Т. и. широко применяется в дифференциальной геометрии, теории римановых пространств, теории относительности, механике, электродинамике и других областях науки.
Для описания многих физических и геометрических фактов обычно вводится та или иная система координат, что позволяет описывать
различные объекты при помощи одного или нескольких чисел, а соотношения между объектами - равенствами, связывающими эти числа или системы чисел.
Некоторые из величин, называемые скалярными (масса, температура и т. д.), описываются одним числом, причём значение этих величин не изменяется при переходе
от одной системы координат к другой (мы рассматриваем здесь физические явления с точки зрения классической физики). Другие величины - векторные
(сила, скорость и т. д.), описываются тремя числами (компонентами вектора), причём при переходе от одной системы координат к другой компоненты вектора
преобразуются по определённому закону. Наряду со скалярными и векторными величинами встречаются во многих вопросах физики и геометрии величины
более сложного строения. Эти величины, называемые тензорными, описываются в каждой системе координат несколькими числами (компонентами тензора),
причём закон преобразования этих чисел при переходе от одной системы координат к другой более сложен, чем для векторов (точные определения будут
даны ниже). При введении координатной системы, помимо чисел, описывающих сам объект или физическое явление, появляются числа, описывающие его связь
с выбранной системой координат. Рассмотрим, например, совокупность чисел Jij (i, j = 1, 2, 3), где Jij - осевой момент инерции
твёрдого тела относительно оси Xi, a Jij, (при i1j) - центробежные моменты инерции, взятые с обратным знаком.
При переходе от одной системы координат к другой осевой момент инерции Jii меняется (так как меняется положение оси xi относительно тела),
а потому Jii не может рассматриваться как физическая величина, имеющая независимый от выбора системы координат смысл.
Это находит своё выражение, например, в том, что знание Jii в одной системе координат не позволяет найти Jii в другой системе координат.
В то же время совокупность всех чисел Jij имеет смысл, независимый от выбора координатной системы. Знание всех чисел Jij
в одной системе прямоугольных координат позволяет найти их в любой другой системе прямоугольных координат по формуле
(
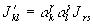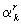и 
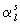- некоторые числа): здесь,
как принято в Т. и., опущен знак суммы и считается, что если один и тот же индекс встречается дважды (один раз наверху, а другой раз внизу),
то по нему производится суммирование, причём этот индекс принимает все возможные для него значения (в приведённом примере - значения 1, 2, 3). Т. и.,
как и векторное исчисление, является математическим аппаратом, при котором исключается влияние выбора координатной системы. Это достигается тем,
что задание компонент тензора в какой-либо системе координат определяет их во всех других системах координат. В Т. и. указываются методы получения
соотношений между тензорами и функций от компонент тензоров, не меняющихся при переходе от одной системы координат к другой (инвариантных соотношений
и инвариантов).
Т.о., одной из основных задач Т. и. является нахождение аналитических формулировок законов механики, геометрии, физики, не зависящих от выбора координатной системы.
Форма выглядит следующим образом:
Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.