Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Линейная интерполяция

    В данном разделе мы рассмотрим самый простой метод нахождения линейной интерполяции таблично заданной функции одного аргумента.

    Интерполяция, интерполирование - в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

    Многим из тех, кто сталкивается с научными и инженерными расчётами, часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией кривой. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

    Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевести получаемую погрешность в результатах.

    Простейшим и часто используемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные точки 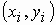при (i = 0. 1, ..., n) соединяются прямолинейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках.

    Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется n интервалов 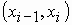, то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точк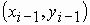и и 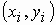, в виде

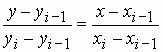
    Отсюда

(*)

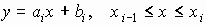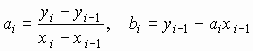
    Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента х, а затем подставить его в формулу (*) и найти приближенное значение функции в этой точке

    Форма выглядит следующим образом:

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.