Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru

На главную Контакты Выполнить расчёт (запустить приложение)

Интерполяционная схема Лагранжа

    Программа позволяет, в зависимости от способа обращения к ней, выполнять интерполяцию, дифференцирование или интегрирование функции одной переменной, заданной таблично, которая на всем или на интересующей нас части интервала адекватно описывается с помощью двухпараболической кривой.

    Алгоритм программы основан на использовании интерполяционной схемы Лагранжа, приспособленной для осреднения парабол второго порядка. По данному методу вычисляется значение, производная и интеграл функции, численно определенной в точках i, i+1, i+2, i+3, путем проведения одной параболы через точки i, i+1, i+2 (y=A₁·x²+ B₁·x+C₁) и второй параболы через точки i+1, i+2, i+3 (y=A₂·x²+B₂·x+C₂ ). Тогда значения в интервале от точки i+1 до точки i+2 определяются с помощью аппроксимационного уравнения второго порядка, коэффициенты которого определяются как среднее арифметическое коэффициентов первого и второго полинома:

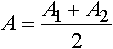
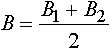
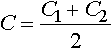
    Дифференцирование осуществляется на основании полученного уравнения по формуле:

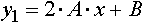
    Интегрирование осуществляется путем суммирования интегралов на полных и неполных участках между точками i+1 и i+2, попадающих на интервал варьирования.

    Точки i, i+1, i+2, i+3 выбираются из таблицы таким образом, чтобы аргумент попадал между точками i+1, i+2.

    Если значения аргумента при интегрировании и дифференцировании или интеграл при интегрировании попадает вне области табличного определения функции x₁...x_n, где n - число точек, то формула Лагранжа работает как экстраполяционная [1126].

    Пример экранной формы.

    Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.