 |
Интеллектуальная среда дистанционного обучения и дизайна http: econom.misis.ru, fdisto.misis.ru; e-mail: vaosadchy@yandex.ru |
| На главную | Контакты | Выполнить расчёт (запустить приложение) |
|
|||
|
3 Теоретическое введение
3.1 Постановка задачи*)
*) Постановка задачи и методика ее решения принадлежат проф. Н.П.Банному
Металлургические заводы А, Б и В снабжаются рудой из одной группы железорудных месторождений.
Рудник Р1 мощностью А1 млн. т в год выдает товарную руду содержанием 62 % Fe, рудник Р2 мощностью А2 млн. т в год - товарную руду с 56 % Fe и рудник Р3 мощностью А3 млн. т в год - товарную руду с 48 % Fe. Содержание примесей и состав пустой породы во всех рудах примерно одинаковы. Заводы А, Б и В расположены на расстоянии соответственно 700, 500 и 300 км от железорудного месторождения. Транспортные расходы на доставку руды на заводы учтены в себестоимости чугуна.
Мощности заводов А по чугуну составляет В1 млн. т; завода Б - В2 млн. т завода В - В3 млн. т в год.
Требуется составить оптимальный план снабжения заводов рудой, при котором себестоимость суммарного объёма производства чугуна трех заводов была бы минимальной.
При разработке плана снабжения заводов рудой необходимо принять во внимание следующие условия:
- ни один из рудников в отдельности по масштабам выдачи товарной руды не может обеспечить железорудным сырьем все три завода;
- желательно поставить все заводы по снабжению в условия, наиболее благоприятные для повышения прибыльности их производства;
- предоставить всем заводам равные условия снабжения рудой;
- создать лучшие условия снабжения более качественной рудой для заводов со сравнительно высокой себестоимостью чугуна с целью улучшить их экономические позиции и тем самым способствовать уменьшению суммарных издержек: трех заводов.
3.2 Методика расчётов
При распределении имеющихся ресурсов товарной руды могут быть использованы как традиционные методы, так и методы линейного программирования с применением компьютерной программы, позволяющей определить оптимальный (наиболее экономичный из всех возможных вариантов при данных условиях) план снабжения заводов рудой.
В качестве примера решим задачу, пользуясь исходными данными, где мощности рудников по товарной руде составляют соответственно: А1 =6 млн. т в год, А2 =10 млн. т в год, А3= 16 млн. т в год, а мощности заводов А, Б и В по чугуну: В1= 5 млн. т в год, В2 = 6 млн. т в год, В3 =5 млн. т в год.
3.3 Определение плана снабжения заводов рудой традиционными способами
Рассмотрим два возможных варианта снабжения заводов рудой, которые могут быть составлены традиционными методами.
Первый метод предусматривает снабжение каждого из заводов всеми сортами руды пропорционально выплавке чугуна. Расчёт поставок руды на заводы при этом производится следующим образом:
1) Для завода А
руда с содержанием 62 % железа
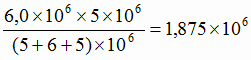 т
т
руда с содержанием 56 % железа
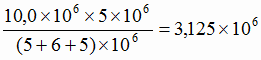 т
т
руда с содержанием 48 % железа
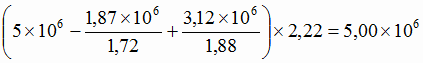 т
т
2) Для завода Б
руда с содержанием 62 % железа
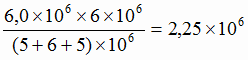 т
т
руда с содержанием 56 % железа
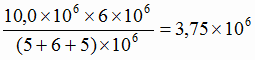 т
т
руда с содержанием 48 % железа
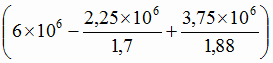
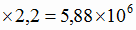 т
т
3) Для завода В
руда с содержанием 62 % железа
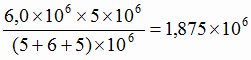 т
т
руда с содержанием 56 % железа
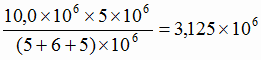 т
т
руда с содержанием 48 % железа
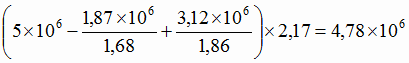 т
т
Снабжение заводов рудами по первому плану можем представить в табл. 3
Таблица 1.3. Количество руды, поставляемой заводам, млн. т
| Заводы | Руда с содержанием железа, % | Всего руды | ||
| 62,0 | 56,0 | 48,0 | ||
| А | 1,875 | 3,125 | 5 | 10 |
| Б | 2,25 | 3,75 | 5,88 | 11,88 |
| В | 1,875 | 3,125 | 4,78 | 9,78 |
| Всего | 6 | 10 | 15,66 | 31,66 |
При таком распределении руды себестоимость всего выпускаемого чугуна будет:
на заводе А
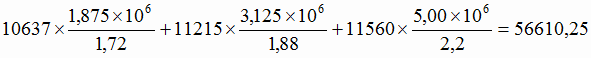 млн. руб.
млн. руб.
себестоимость 1 т чугуна 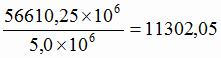 руб.
руб.
на заводе Б
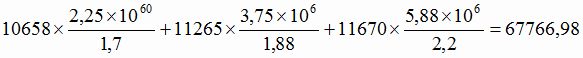 млн. руб.
млн. руб.
себестоимость 1 т чугуна 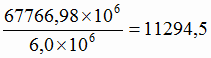 руб.
руб.
на заводе В
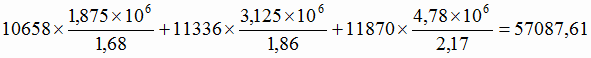 руб.
руб.
себестоимость 1 т чугуна 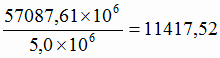 руб.
руб.
Себестоимость всего выпуска чугуна на 3-х заводах составит
56610,25 + 67766,98 + 57087,61 = 181464,84 млн. руб.
себестоимость 1 т чугуна
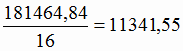 руб./т
руб./т
Второй метод предусматривает снабжение заводов А и Б в той очередности рудами из рудников Р1 и Р2 в размерах, определяемых мощностью последних. Расчёт поставок руды на заводы в этом случае производится следующим образом:
1) для завода А потребуется руды с содержанием 62 % железа:
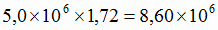 т
т
Однако объём добычи этой руды на руднике Р1 составляет лишь 6,0 млн. т. Следовательно, поставка руды с содержанием 62 % железа на завод А составит 6,0 млн. т, что обеспечит выпуск чугуна в количестве
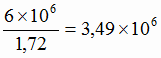 т
т
Для обеспечения выплавки оставшихся 1,51 млн. т (5,0×106 - 3,49×106) потребуется 2,86×106 т (1,52×106×1,88=2,86×106) для руды с содержанием 56 % железа.
Таким образом для завода А поставки руды с содержанием 62 % железа составит 6,0 ×106 т, с содержанием 56 % железа - 2,86 ×106 т.
Аналогично проводятся расчёты поставок для заводов Б и В. Распределение руды по заводам по второму плану снабжения представлено в табл. 4.
Таблица 1.4. Количество руды, поставляемой заводам, млн. т
| Заводы | Руда с содержанием железа, % | Всего руды | ||
| 62,0 | 56,0 | 48,0 | ||
| А | 6 | 2,83 | - | 8,83 |
| Б | - | 7,16 | 4,81 | 11,97 |
| В | - | - | 10,85 | 10,85 |
| Всего | 6 | 10 | 15,66 | 31,65 |
При таком распределении руды себестоимость всего выпускаемо чугуна будет:
на заводе А 53987,97 млн. руб. и средняя себестоимость 1 т 10797,59 руб.
на заводе Б 68477,66 млн. руб. и средняя себестоимость 1 т 11412,94 руб.
на заводе В 59350,00 млн. руб. и средняя себестоимость 1 т 11870,00 руб.
Себестоимость годового объёма производства чугуна всех трех заводов составит 181815,62 млн. руб. и средняя себестоимость 1 т чугуна 11363,48 руб.
Сравнительный анализ вариантов показывает, что первый план распределения руды лучше первого, так как суммарные текущие расходы на выплавку 16,0 млн. т чугуна на заводах меньше на 350,78 млн. руб. Улучшаются экономические показатели заводах Б и В, на которых себестоимость 1 т чугуна снижается соответственно на 118,45 руб. и 452,48 руб. Однако при этом ухудшается экономика на заводе А, где себестоимость чугуна увеличивается на 504,46 руб. (4,5 %). Правомерно поставить вопрос: является ли первый план распределения самым лучшим, нельзя ли найти такое распределение руды между заводами, при котором средняя цена чугуна будет стоить меньше, чем по первому плану. Это можно установить лишь, решая поставленную задачу с помощью методов линейного программирования с использованием компьютера. С этой целью следует разработать экономико-математическую модель (ЭММ) задачи.
3.4 Разработка экономико-математической модели определения оптимального плана снабжения завода рудой.
Введем следующие обозначения:
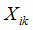 - количество (неизвестное, искомое) руды i -го сорта, необходимое для выплавки чугуна на k-ом заводе, т;
- количество (неизвестное, искомое) руды i -го сорта, необходимое для выплавки чугуна на k-ом заводе, т;
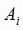 - мощность i-го рудника по товарной руде, т;
- мощность i-го рудника по товарной руде, т;
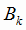 - мощность k -того завода по чугуну, т;
- мощность k -того завода по чугуну, т;
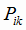 - количество руды i-го сорта, необходимое для выплавки 1 т чугуна на k-ом заводе (расходный коэффициент), т/т;
- количество руды i-го сорта, необходимое для выплавки 1 т чугуна на k-ом заводе (расходный коэффициент), т/т;
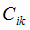 - себестоимость чугуна, выплавленного из руды i -го сорта на k-ом заводе, руб./т.
- себестоимость чугуна, выплавленного из руды i -го сорта на k-ом заводе, руб./т.
Опишем ЭММ задачи в общем виде:
1) для обеспечения условия не превышения мощности рудников необходимо, чтобы выполнялись следующие неравенства:
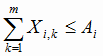 (i = 1, 2,
3... n) (i = 1, 2,
3... n) |
(1.1) |
2) условие полной загрузки заводов описывается уравнениями типа:
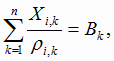 (k=1, 2, 3 …. m) (k=1, 2, 3 …. m) |
(1.2) |
3) все Xik по смыслу положительные величины, т.е.
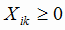 , , |
(1.3) |
4) необходимо отыскать такие значения Xik, чтобы обратилась в минимум следующая линейная форма:
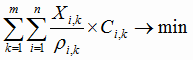 |
(1.4) |
Система уравнений (1)-(4) представляет собой экономико-математическую модель задачи в общем виде. В этой модели уравнения (1)-(3) описывают условия задачи и называются ограничениями, а уравнение (4) описывает цель задачи и называется целевой функцией.
Рассмотрим применение метод линейного программирования на конкретном примере, пользуясь исходными данными варианта № 30, приведенными в табл. 1.1 и 1.2 индивидуальных вариантов заданий, где мощности А1, А2 и Аз рудников Р1, P2 и P3 по товарной руде соответственно 6, 10 и 16 млн. т. в год, а мощности Р1, Р2, и P3 заводов А, Б и В по чугуну соответственно 5, 6 и 5 млн. т в год.
Подставляя известные численные значения коэффициентов Ai, Bk, Pik, Cik в развернутую систему уравнений получают экономико-математическую модель для определения оптимального варианта плана. Так, для нашего примера экономико-математическая модель задачи будет описываться следующей системой уравнений:
Ограничения по мощности рудников.
1. 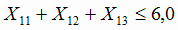
2. 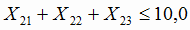
3. 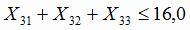
Ограничения по выпуску чугуна
4. 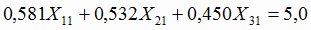
5. 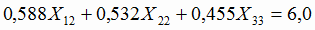
6. 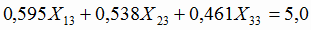
В п.п. 4-6 коэффициенты рассчитываются как обратные величины расходному коэффициенту (1/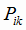 ), т.е.
выход годного.
), т.е.
выход годного.
7. 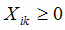
8. Целевая функция:
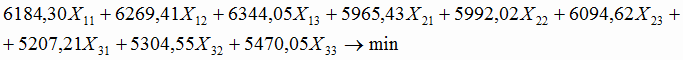
В п. 8 коэффициенты рассчитываются следующим образом: выход годного для руды 1 на заводе А умножается на себестоимость чугуна завода А для этой руды; выход годного для руды 1 на заводе Б умножается на себестоимость чугуна завода Б для этой руды и т.д.
Решая задачу на ЭВМ, получаем оптимальный план снабжения заводов рудой, который представлен в табл. 1.5.
Таблица 1.5. Оптимальный план снабжения заводов рудой, млн.т.
| Рудники | А | Б | В | Руда |
| Р1 | 0,00 | 0,00 | 6,00 | 6,00 |
| Р2 | 0,00 | 7,34 | 2,66 | 10,00 |
| Р3 | 11,10 | 4,61 | 0,00 | 15,71 |
| Чугун | 11,10 | 11,95 | 8,66 | 31,71 |
Таким образом, на завод А отправляется руда в количестве 11,1 млн. т рудника Р3. На завод Б поступает руда с рудника Р2 в количестве 7,34 млн. т и с рудника Р3 - 4,61 млн. т. На завод В поступает руда с рудника Р1 в количестве 6 млн. т и с рудника Р2 2,66 млн. т. При этом на руднике Р3 остается в резерве 0,29 млн. т руды.
При таком распределении руды себестоимость чугуна на заводах составляет:
- заводе А 11560 руб./т
- заводе Б 11406,36 руб./т
- заводе В 10851,71 руб./т
- средняя себестоимость чугуна на всех трех заводах - 11281,05 руб./т.
Себестоимость годового объёма производства чугуна на всех трех заводов (значение целевой функции) - 180,5 млрд. руб.
Вывод. Применение методов линейного программирования и ЭВМ для решения подобных задач позволяет определить оптимальный план снабжения заводов рудой (или другими материальными ресурсами), при котором получаются минимальные суммарные текущие затраты на заводах.
По сравнению с лучшим планом, разработанным традиционными методами вручную (вариант I), оптимальный план дает экономию за счёт снижения суммарных текущих затрат на производство 968,11 млн. т чугуна.