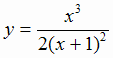 и построим её график.
и построим её график.Главная страница Предыдущая страница
3 Примеры выполнения типового расчёта
Задача 1. Исследуем функцию 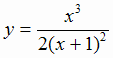 и построим её график.
и построим её график.
Решение. 1. Функция определена на всей числовой прямой, кроме точки 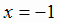 , в которой знаменатель
дроби обращается в нуль, т. е.
, в которой знаменатель
дроби обращается в нуль, т. е. 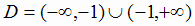 ;
; 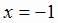 - точка разрыва.
- точка разрыва.
2. Функция заведомо не обладает свойствами четности или нечетности, так как её область определения не симметрична относительно начала координат. Поэтому исследование функции нужно выполнять на всей числовой прямой.
3. Найдем точки пересечения графика функции 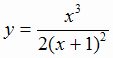 с осями координат. При
с осями координат. При 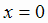 получим у = 0, т. е. О (0; 0). В этой точке график пересекает обе координатные оси.
получим у = 0, т. е. О (0; 0). В этой точке график пересекает обе координатные оси.
4. Помечаем знаками + и - интервалы, на которых функция принимает соответственно положительные и отрицательные значения (рис. 2.11)
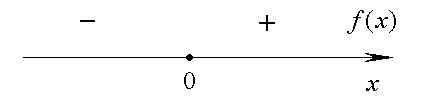
Рис. 2.11.
5. В точке разрыва х = - 1 существует вертикальная асимптота х = - 1, так как 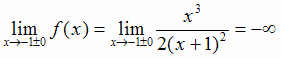 .
.
Горизонтальной асимптоты график не имеет, поскольку
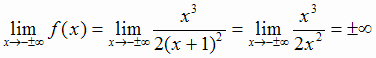
Выясним наличие наклонных асимптот:
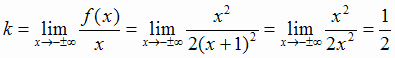
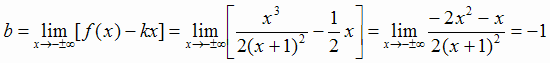 .
.
Пределы, определяющие k и b, совпадают при 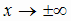 , поэтому
, поэтому 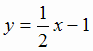 -
двусторонняя наклонная асимптота кривой.
-
двусторонняя наклонная асимптота кривой.
6. Имеем 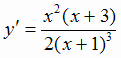 . Критические точки находим из условия у' = 0, откуда
. Критические точки находим из условия у' = 0, откуда 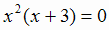 ,
т.е. х = - 3 и х = 0. Функция может переходить от возрастания к убыванию или наоборот в критических точках
,
т.е. х = - 3 и х = 0. Функция может переходить от возрастания к убыванию или наоборот в критических точках 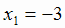 ;
;
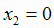 и в точке разрыва х = - 1. Эти точки разбивают область определения на четыре интервала монотонности:
и в точке разрыва х = - 1. Эти точки разбивают область определения на четыре интервала монотонности: 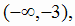
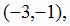

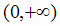 . На рис. 2.12 показаны знаки
. На рис. 2.12 показаны знаки 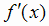 в этих интервалах.
в этих интервалах.
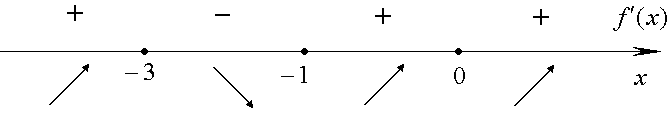
Рис. 2.12.
Согласно достаточному признаку экстремума, х = - 3 - точка максимума; при х = 0 экстремума нет. Соответствующие
значения функции составляют  ,
, 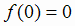 . Касательная в точке максимума горизонтальна, так как
. Касательная в точке максимума горизонтальна, так как 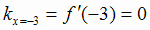 .
.
7. Имеем  , поэтому все возможные точки перегиба находим из уравнения
, поэтому все возможные точки перегиба находим из уравнения ,
т. е. х = 0. Направление выпуклости кривой может изменяться в точках перегиба и в точках разрыва функции. Точка разрыва х = -
1 и возможная точка перегиба х = 0 разбивают всю область определения на три интервала
,
т. е. х = 0. Направление выпуклости кривой может изменяться в точках перегиба и в точках разрыва функции. Точка разрыва х = -
1 и возможная точка перегиба х = 0 разбивают всю область определения на три интервала 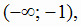
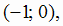
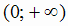 , внутри которых направление выпуклости не меняется. Знаки у" в этих интервалах показаны на рис. 2.13.
, внутри которых направление выпуклости не меняется. Знаки у" в этих интервалах показаны на рис. 2.13.
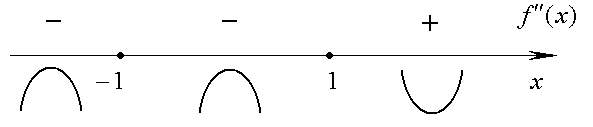
Рис. 2.13.
В интервалах 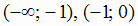 кривая выпукла вверх. В точке х = 0 кривая меняет выпуклость вверх на выпуклость
вниз; так как f (0) = 0, то О(0; 0) - точка перегиба графика. Угловой коэффициент касательной в этой точке
кривая выпукла вверх. В точке х = 0 кривая меняет выпуклость вверх на выпуклость
вниз; так как f (0) = 0, то О(0; 0) - точка перегиба графика. Угловой коэффициент касательной в этой точке 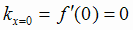 ,
поэтому касательная в точке перегиба горизонтальна и совпадает с осью Ох.
,
поэтому касательная в точке перегиба горизонтальна и совпадает с осью Ох.
8. Помечаем на чертеже точку пересечения с осями координат, она же точка перегиба, точку экстремума. Строим асимптоту, а затем график исследуемой функции (рис. 2.14).
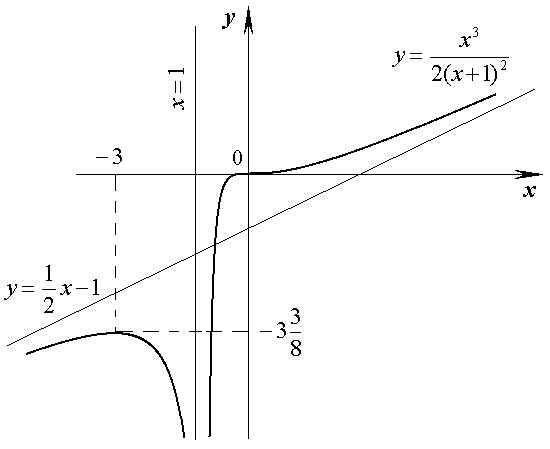
Рис. 2.14.
Задача 2. Исследуем функцию 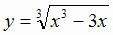 и построим её график.
и построим её график.
Решение. 1. Функция определена и непрерывна на всей числовой прямой.
2. Так как 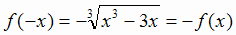 , то функция нечетная. Её график симметричен относительно начала координат,
поэтому исследование можно выполнить только для
, то функция нечетная. Её график симметричен относительно начала координат,
поэтому исследование можно выполнить только для 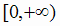 .
.
3. Разложим подкоренное выражение на множители
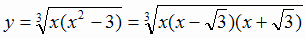 .
.
Функция равна нулю при 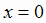 и
и 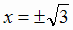 . Помечаем эти точки на оси Ox (рис. 2.15).
. Помечаем эти точки на оси Ox (рис. 2.15).
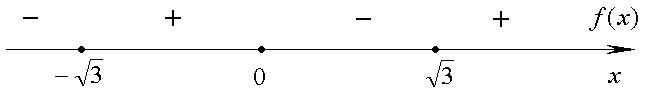
Рис. 2.15.
4. Помечаем знаками + и - интервалы, на которых функция принимает, соответственно, положительные и отрицательные значения (рис. 3.28)
5. Вертикальных асимптот нет, так как функция непрерывна на всей числовой прямой. Горизонтальных асимптот также нет, поскольку

Выясним наличие наклонных асимптот:
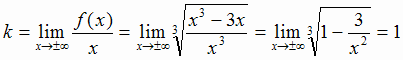
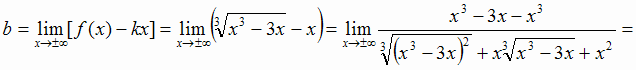
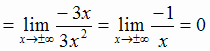
График имеет двустороннюю наклонную асимптоту у = х.
6. Находим 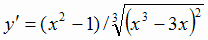 . Раскладываем производную на множители:
. Раскладываем производную на множители:
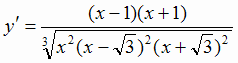
Решая уравнение у' = 0, получаем х = ± 1; из условия 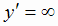 имеем
имеем 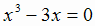 ,
т. е.
,
т. е.  и
и 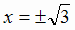 . Исследуем знаки производной в интервалах
. Исследуем знаки производной в интервалах 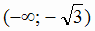 ,
,
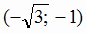 ,
, 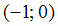 ,
, 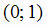 ,
, 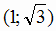 ,
, 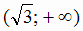 .
В этих интервалах знаки
.
В этих интервалах знаки 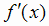 изменяются так, как показано на рис. 2.16. Отсюда следует, что при х = 1 функция имеет
минимум
изменяются так, как показано на рис. 2.16. Отсюда следует, что при х = 1 функция имеет
минимум 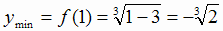 , а
, а 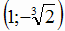 - точка минимума графика. Так как функция нечетная,
то в точке
- точка минимума графика. Так как функция нечетная,
то в точке 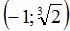 функция имеет максимум. Касательная в точках экстремума горизонтальна, поскольку
функция имеет максимум. Касательная в точках экстремума горизонтальна, поскольку 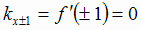 .
.

Рис. 2.16.
7. Находим 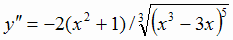 . Раскладываем вторую производную на множители:
. Раскладываем вторую производную на множители:
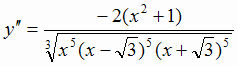
Из полученного выражения видно, что 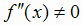 . Из условия
. Из условия 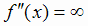 имеем
имеем 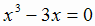 ,
откуда
,
откуда  и
и 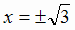 . Исследуем знаки
. Исследуем знаки  в интервалах
в интервалах 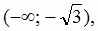
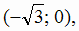

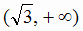 . Знаки
. Знаки  в этих интервалах показаны на рис. 2.17.
в этих интервалах показаны на рис. 2.17.
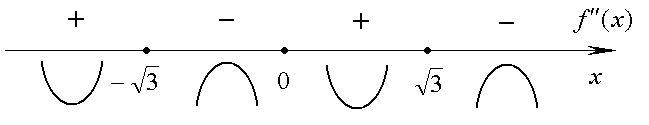
Рис. 2.17.
Отсюда следует существование точек перегиба при х = 0 и при 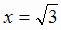 и, в ввиду центральной симметрии
графика, при
и, в ввиду центральной симметрии
графика, при 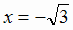 .Так как
.Так как 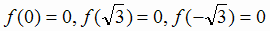 , то
, то 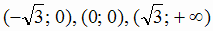 - точки
перегиба графика. Касательные к графику в точках перегиба вертикальны, поскольку
- точки
перегиба графика. Касательные к графику в точках перегиба вертикальны, поскольку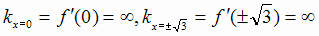 . Точки перегиба оказались
одновременно точками пересечения графика о осями координат.
. Точки перегиба оказались
одновременно точками пересечения графика о осями координат.
8. Помечаем на чертеже точки пересечения с осями координат, они же точки перегиба, точки экстремума. Строим асимптоту, а затем график исследуемой функции (рис. 2.18).
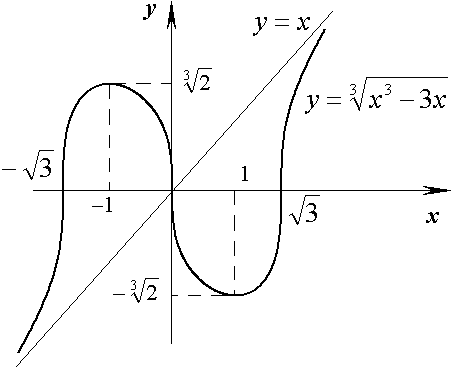
Рис. 2.18.